Important Results in Context with Rotation

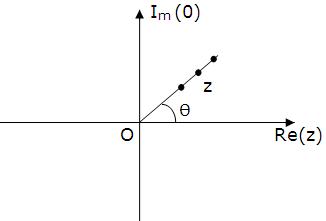
 (i) arg z = 0 represents points (non-zero) on a ray emanating from origin making an angle θ with positive direction of real axis.

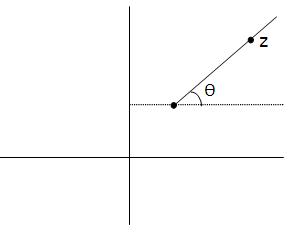
(ii) arg (z-z₁)= 0 represents points ( ≠3,) on ray emanating from z, making an angle θ with positive direction of real axis.

Rotation theorem:

(i) If P(z₁) and Q(z₂) are two complex numbers such that |z₁| = |z₂|, then z₂=z₁ e^iθ,  where θ = ⁄POQ.

(ii) If P(z₁), Q(z₂) and R(z₃) are three complex numbers and ⁄PQR=Q, then

 (iii) If P(z₁), Q(z₂), R(z₃) and S(z₄) are three complex numbers and ⁄STQ= θ, then

2. amp (z) = θ is a ray emanating from the origin inclined at an angle θ to the x-axis.

3. |z-a|=|z-b| is the perpendicular bisectors of the line joining a to b.

4. The equation of a line joining z₁ and z₂ is given by z = z₁ + t(z₁-z₂) where t is a real parameter.

5. z = z₁ (1+it) where t is a real parameter is a line through the point z, and perpendicular to the line joining z, to the origin.

6. The equation of a line passing through z₁ and z₂ can be expressed in the determinant form as

This is also the condition for three complex numbers z, z₁, z₂ to b collinear.

7. The equation of a circle having centre z₀ and radius p is:

         |z-z₀| = p or z   - z₀- 0 - z + 0z₀ - p² = 0 which is of the form

         z + z + α + k = 0, k is real.

         Centre is -α  and radius =√(α - k)  circle will be real if α - k ≥ 0.

8. The equation of the circle described on the line segment joining z1 and z2 as

diameter is arg (z-z₂)/(z-z₂ )= ±Π/2 or (z-z₁) (-₂)+(z-z₂ )(₁)=0

9. Condition for four given points z1, z2, z3 and z4 to be concyclic is the number

(z₃ z₁)/(z₃-z₂ ).(z₄ z₂)/(z₄-z₁ ) should be real.

Hence, the equation of a circle through 3 non-collinear points z1, z2 and z3 can be taken as

(z-z₁ )(z₃-z₁ )/((z-z₁ )(z₃-z₂)) is real 

=>  (z-z₂ )(z₃-z₁ )/((z-z₁ )(z₃-z₂))=(-₂ )(₃- ₁)/((z-z₁ )(z₃-z₂))

10. Arg((z-z₁)/(z-z₂)) = 0  represent

(i) a line segment if θ =Π

(ii) pair of ray if θ = 0

(iii) a part of circle, if 0<0<Π

11. Area of triangle formed by the points z₁, z₂ and z₃ is

12. Perpendicular distance of a point z₀ from the line

         z + α + r = 0  is |( z0 + α + r )/α|α||

13. (i) Complex slope of a line z + α + r = 0  w = - α/α

        (ii) Complex slope of a line joining the points z₁ and z₂ is w=(z1-2)/(z1-2)

        (iii) Complex slope of a line making Q angle with real axis w=l^2iθ

14. Dot and Cross product

Let z1 = x₁ + i y₁ and z₂ = x₂ + i y₂ be two complex numbers (vectors). The dot product (also called the scalar product) of z₁ and z₂ is defined by z₁.z₂ = |z₁| |z₂| cos θ

                                = x₁x₂ + y₁y= = Re {1z2}

                                = 1/2{1z2 + z₁2}

Where θ is the angle between z1 and z2 which lies between 0 and Π .

If vectors z₁, z₂ are perpendicular then z₁.z₂ = 0 => z₁/z₂ + z₂/z₂ = 0

i.e. sum of complex slopes = 0

The cross product of z₁ and z₂ is defined by

        z₁ × z₂ = |z₁| |z₂| sin θ|

                = x₁y₂ - y₁x₂

                = Im{₁z₂ }

                = 1/zi (z₂ - z₁₂)

If vectors z₁, z₂ are parallel then z₁ × z₂ = 0 z₁/z₂ = z₂/z₂

i.e., complex slopes are equal. 

Note:

w₁ and w₂ are complex slopes of two lines.

(i) If lines are parallel then w₁ = w₂

(ii) If lines are perpendicular then w₁ + w₂ = 0

15. If |z-z₁| + |z-z₂| = K> |z₁-z₂| then locus of z is an ellipse focii are z₁ and z₂.

16. If |z-z₀| =  |z + α + r/2K1| then locus of z is parabola whose focus is z₀ and directrix is the line

        z + α + r = 0 (provided z0+ α0 + r ≠ 0)

17. If |(z-z₁)/(z-z₂)| = k < |z₁-z₂|   then locus of z is a circle

18. If  then locus of z is a hyperbola, whose focii are z₁ and z₂.

To read more, Buy study materials of Complex Numbers comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.