Degree of Dissociation

Table of Content

Degree of Dissociation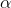
Dependence of Degree of Dissociation from Density Measurements
Thermodynamics of Chemical Equilibrium
Related Resources

Degree of Dissociation ( $\alpha$ )

The degree of dissociation of a substance is defined as the fraction of its molecules dissociating at a given time.

Let us consider the reaction,

2NH₃ (g) $\rightleftharpoons$ N₂ (g) + 3H₂ (g)

Let the initial moles of NH₃(g) be ‘a’. Let x moles of NH₃ dissociate at equilibrium.

Degree of dissociation (a) of NH₃ is defined as the number of moles of NH3 dissociated per mole of NH3.

if x moles dissociate from ‘a’ moles of NH₃, then, the degree of dissociation of NH3 would be x/a.

We can also look at the reaction in the following manner.

In this way you should calculate the basic equation. So my advice to you is that, while solving problem follow the method given below:

Write the balanced chemical reaction (mostly it will be given)
Under each component write the initial no. of moles.
Do the same for equilibrium condition.
Then derive the expression.

Dependence of Degree of Dissociation from Density Measurements

?Refer to the following video for Vapour density and degree of dissociation

The following is the method of calculating the degree of dissociation of a gas using vapour densities. This method is valid only for reactions whose K_P exist, i.e., reactions having at least one gas and having no solution.

Since

pV = nRT

pV = $\frac{w}{M}$ nRT

$M = \frac{wRT}{pV} = \rho \frac{RT}{P}$

$VD =\rho \frac{RT}{2P}$

Since

P = NRT / V

$VD =\rho \frac{RT}{2nRT}\times V =\rho \frac{V}{2n}$

For a reaction at equilibrium V is a constant and ρ is a constant. vapour Density α 1/n

(molecular weight = 2 × V.D)

Here M = molecular weight initial

m = molecular weight at equilibrium

Let us take a reaction

PCl₅ PCl₃ + Cl₂

Initial moles C 0 0

At eqb. C(1-α) Cα Cα

∴ = C(1+α) / C = D/d; 1 + α = D/d = M/m

Knowing D and d, α can be calculated and so for M and m.

Thermodynamics of Chemical Equilibrium

Let ΔG⁰ be the difference in free energy of the reaction when all the reactants and products are in the standard state and K_c or, K_p be the thermodynamic equilibrium constant of the reaction. Both related to each other at temperature T by the following relation.

ΔG⁰ = – 2.303 RT logK_cand ΔG⁰= – 2.303 RT log K_p(in case of ideal gases)

Now, we know that thermodynamically,

ΔG⁰ = ΔH⁰ – TDS⁰

here ΔH⁰ is standard enthalpy of reaction, and ΔS⁰ is standard entropy change

(i) When ΔG⁰ = 0, then, K_c = 1

(ii) When, ΔG⁰ > 0, i.e. +ve, then K_c < 1, in this case reverse reaction is feasible showing thereby a less concentration of products at equilibrium rate.

(iii) When ΔG⁰ < 0, i.e. -ve, then, K_c > 1; In this case, forward reaction is feasible showing thereby a large concentrations of product at equilibrium state.

At equilibrium,

Example 1. When PCl₅ is heated it dissociates into PCl₃ and Cl₂. The density of the gas mixture at 200^oC and at 250^oC is 70.2 and 57.9 respectively. Find the degree of dissociation at 200^oC and 250^oC.

Solution: PCl₅(g) → PCl₃(g) + Cl₂(g)

We are given the vapour densities at equilibrium at 200^oC and 250^oC.

The initial vapour density will be the same at both the temperatures as

it would be M_PCl5 / 2.

∴ Initial vapour density = (31 + 5 × 35.5) / 2 = 104.25

Vapour density at equilibrium at 200^oC = 70.2

∴ Total moles at equilibrium / Total moles initial = 1 + α = Vapour density initial / Vapour density at equilibrium = 104.25 / 70.2 = 1.485

∴ a = 0.485

At 250^oC, 1 + α = 104.25 / 57.9 = 1.8

∴ a = 0.8

Sample problem.

The degree of dissociation of PCl₅ is 60%, then find out the observed molar mass of the mixture.

Solution: PCl_5(g) PCl_3(g) + Cl_2(g)

Initially moles 1 0 0

At eqm. 1 – α α α

Where α = degree of dissociation = 0.6

Total moles at equilibrium = 1 + a = observed mole

$\frac{Observed\ moles}{Theortical \ Moles}=\frac{Theortical\ Molecular\ Weight}{Observed\ Molecular\ Weight}$

$\Rightarrow$ 1 + a = 206.5 / molecular weight observed

$\Rightarrow$ molecular weight observed = 206.5 / 1 + a = 206.5 / 1.6 = 129.06

Example 2. A system is in equilibrium as PCl₅ + Heat —> PCl₃ + Cl₂

Why does the temperature of the system decreases, when PCl₃ are being removed from the equilibrium mixture at constant volume?

Solution: When PCl₃ are being removed from the system, the reaction moved to the right. This consumed heat and therefore, temperature is decreased.

Example. NO and Br₂ at initial partial pressures of 98.4 and 41.3 torr, respectively, were allowed to react at 300K. At equilibrium the total pressure was 110.5 torr. Calculate the value of the equilibrium constant and the standard free energy change at 300K for the reaction 2NO(g) + Br₂(g) 2NOBr(g).

Solution:

2NO(g) + Br₂(g) → 2NOBr(g)

Initial pressure 98.4 41.3 0

At eqlbm. 98.4-x 41.3 - x/2 x

The total pressure at equilibrium is 110.5 torr.

98.4-x + 41.3- x/2 + x = 110.5

x = 58.4 torr

Now, 1 atm = 760.4 torr,

x = 7.68 × 10^-2 atm.

p_NOBr = 7.68 × 10^-2 atm ; p_NO = 98.4-x = 40 torr = 5.26 × 10^-2 atm.

p_Br2 = 41.3 – x/2 = 12.1 torr = 1.59 × 10^-2 atm.

ΔG^o = -2.303 RT log K = -2.303 (1.99) (300) (log 134)

= -2.92 k cal = -12.2 kJ.

[If R is used as 1.99 cal/mol K, then ΔG^o will be in cal. If R is used as 8.314 J/mol K, then ΔG^o will be in Joules. But K_P must always be in (atm)^Δⁿ.]

Related Resources

JEE Chemistry Syllabus

Chemistry Reference Books

To read more, Buy study materials of Chemical Equilibrium comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.