Basic Concepts of Ellipse

 

Table of Content

Major and Minor Axes Semi-major and Semi-minor Axes Pause Central Curve Another definition of an ellipse Other Forms Position of a Point Relative to an Ellipse Area of an Ellipse

When an egg is sliced obliquely, a typical curve appears by its edge. The movement of earth around sun also traces a similar but a larger curve. This special curve is called ellipse. Now we proceed towards the mathematical definition of ellipse:

 An ellipse is locus of a point, which moves in a plane such that the ratio of its distances from a fixed point and a fixed line is constant and always less than one.

In other words "Ellipse" is a conic for which the eccentricity e < 1. Let S be the focus of ellipse, P any point on the ellipse and PM perpendicular distance of the directrix from P, then

     SP/PM = e < 1
 

Major and Minor Axes

By major axis, we mean the longest diameter. The axis which goes form one side of an ellipse to another passing through the center but along the widest part of the ellipse is called the major axis. Similarly, the minor axis is the shortest diameter that lies along the narrowest part of the ellipse.
 

Semi-major and Semi-minor Axes

The Semi-major Axis is half of the Major Axis, and the Semi-minor Axis is half of the Minor Axis.

Let S be the focus and ZM be the directrix of the ellipse. Let e be its eccentricity.

We draw SZ perpendicular to the directrix and divide SZ internally and externally in the ratio e: 1 and let A and A' be the internal and external point of division.

Then we have SA = e AZ                                ...... (1)

  And SA' = e A'Z                                            ...... (2)

 .·. A and A' lie on the ellipse.

 Let AA' = 2a and take O the midpoint of AA' as origin. Let P(x, y) be any point on the ellipse referred to OA and OB as co-ordinate axis.

Then from figure it is evident that

AS = AO - OS = a - OS

AZ = OZ - OA = OZ - a

A'S = A'O + OS = a + OS

A'Z = OZ + OA' = OZ + a

Substituting these values in (1) and (2), we have

a - OS = e (OZ - a)                                    ...... (3)

a + OS = e (OZ + a)                                  ...... (4)

Adding (3) and (4), we get

2a = 2 e OZ

Or     OZ = a/e                                                 ...... (5)

Subtracting (3) from (4), we get

2 OS = 2ae => OS = ae                                ...... (6)

.·. The directrix MZ is x = OZ = a/e and the co-ordinate of the focus S are (OS, 0) i.e. (ae, 0). Now as P(x, y) lies on the ellipse.

So we get

SP = e PM or SP² = e² PM²

(x - ae)² + y² = e² [OZ - x co-ordinate of P]²

=> (x - ae)² + y² = e² [a/e - x]² = (a - ex)²      ...... (7)

=> x² + a²e² - 2axe + y² = a² + e²x² - 2aex

or  x²/a² + y²/a²(1-e²) = 1    [Dividing each term by a² (1 - e²)]

or  x²/a² + y²/b² = 1 where b² = a² (1 - e²)

This is the standard equation of an ellipse, O is called the center of the ellipse, AA' and BB' are called the major and minor axes of ellipse (where b < a).

There exists a second focus and second directrix for the curve. On the negative side of the origin take a point S', which is such that SO = S'O = ae and another point Z' such that ZO = OZ' = a/e.

Draw Z'K' perpendicular to ZZ' and PM' perpendicular to Z'K'

The equation (7) may also be written in the form

(x + ae)² + y² = (a + ex)²

=>  S'P² = e² (PM')²

Hence, any point P on the curve is such that its distance from S' is e times to its distance from Z'K' so we should have obtained the same curve, if we had started with S' as focus, a Z'K' as directrix and the same eccentricity.
 

Pause

We have considered a > b, now if we consider b > a, what will be the shape of the ellipse x²/a² +y²/b²? In this case the major axis AA' of the ellipse is along the y-axis and is of length 2b. See figure.

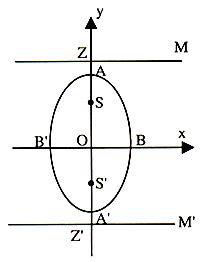
The minor axis of BB' = 2a. The foci S and S' are (0, be) and (0, -be) respectively. The directrix are MZ and M'Z' given by y = + b/e, respectively. Also here a² = b² (1 - e²).

Note:

Let P(x₁, y₁) be any point. This point lies outside, on or inside the ellipse (8) according as x²₁/a² + y²₁/b² = 1 > 0 or = 0 or < 0.
 

Central Curve

A curve is said to be a central curve if there is a point, called the centre, such that every chord passing through it is bisected at it.

Latus rectum:

The length of a chord through the focus and at right angle to the major axis of the ellipse is known as the latus rectum of the ellipse.

There being two foci of an ellipse, there are two rectum, which are of equal length.

 yL = b²/a

.·. The length of latus rectum LSL' = 2b²/a

Notes:

• The major axis AA' is of length 2a and the minor axis BB' is of length 2b.

• The foci are (-ae, 0) and (ae, 0).

• The equations of the directrices are x = a/e and x = -a/e.

• The length of the semi latus rectum = b²/a.

• Circle is a particular case of an ellipse with e = 0.

Focal Distance of a Point

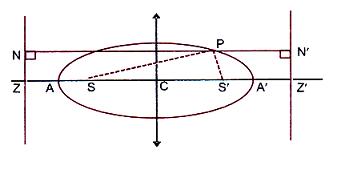
Since S'P = ePN', SP = ePN,

S'P + SP = e (PN + PN')

=      e (NN') = e (2a/e) = 2a

=>    The sum of the focal distances of any point on the ellipse is equal to its major axis.

You can get an idea about the type of questions asked by seeing the  past year papers.

Another definition of an Ellipse

Let ellipse be x²/a² +y²/b² = 1                                               ...... (i)

Its foci S and S' are (ae, 0) and (-ae, 0). The equation of its directrices MZ and M'Z' are x = a/e and x = -a/e respectively. Let P(x₁, y₁) be any point on (i)

Now SP = e PM = e NZ = e (OZ - ON) = e[(a/e)-x₁] = a - ex₁

and S'P = ePM' = e (Z'N) = e (OZ' + ON) = e[(a/e) + x₁] = a + ex₁ 

.·. SP + S'P = 2a = AA'

So by this property an ellipse can also be defined as "the locus of a point which moves such that the sum of its distances from two fixed point is always constant.
 

Other Forms

• If in the equation x²/a² +y²/b² = 1, a² < b², then the major and minor axis of the ellipse lie along the y and the x-axis and are of lengths 2b and 2a respectively. The foci become (0, + be), and the directrices become y = + b/e where e = √(1-a²/b² ). The length of the semi-latus rectum becomes a²/b².

• If the centre of the ellipse be taken at (h, k) and axes parallel to the x and the y-axes, then the equation of the ellipse is (x-h)²/a² +(y-k)²/b² = 1.

• Let eh equation of the directrix of an ellipse be ax + by + c = 0 and the focus be (h, k).

 Let the eccentricity of the ellipse be e (e < 1).

If P(x, y) is any point on the ellipse, then

PS² = e² PM²

=>  (x - h)² + (y - k)² = e²(ax+by+c)²/(a² + b² ), , which is of the form

ax² + 2hxy + by² + 2gx + 2fy + c = 0 ... (*) where

Δ = abc + 2fgh + af² - bg² - ch² ≠ 0, h² < ab.

These are the necessary and sufficient conditions for a general quadratic equation given by (*) to represent an ellipse.

 For more, look into the video

Position of a Point Relative to an Ellipse

The point P(x₁, y₁) is outside or inside the ellipse x²/a² + y²/b² =  1, according as the quantity ((x₁²)/a² +(y₁²)/b² -1)  is positive or negative.

Parametric Equation of an Ellipse

Clearly, x = a cosθ, y = b sinθ satisfy the equation x²/a² +y²/b²   = 1 for all real values of θ.

Hence, the parametric equations of the ellipse  x²/a² +y²/b² = 1 are x = a cosθ, 
y = b sinq where θ is the parameter.

Also (a cos θ, b sin θ) is a point on the ellipse  x²/a² +y²/b² = 1 for all values of 
θ(0 < θ < 2Π).

The point (a cosθ, b sinθ) is also called the point θ. The angle θ is called the eccentric angle of the point (a cosθ, b sinθ) on the ellipse.

Draw a circle with AA' (the major axis) as the diameter. This circle is called the auxiliary circle of the ellipse. The equation of the circle is x² + y² = a². Any point Q on the circle is (a cosθ, a sinθ). Draw QM as perpendicular to AA' cutting the ellipseat P. The x-co-ordinate of P = CM = a cosθ.

=>  y-co-ordinate of P is b sinθ

=>  P ≡ (a cosθ, b sinθ).
 

Area of an Ellipse

Suppose j is the major axis of the ellipse and n is the minor axis. Then the area of the ellipse is given by the formula

Area=π jn

Illustration:

Find the equation of an ellipse centered at the origin with major axis of length 10 lying along the x-axis and minor axis of length 6 along the y-axis.
Solution:

The major axis has length 10 along the x-axis and is centered at (0, 0), so its

endpoints are at (-5,0) and (5,0). 

Hence, we get a = 5 and b = 3. So the required equation of the ellipse is

x²/5² + y²/ 3² = 1 or x² / 3² + y²/ 5² = 1.

Illustration:

Find the equation of the ellipse, which cuts the intercept of length 3 and 2 on positive x and y-axis. Centre of the ellipse is origin and major and minor axes are along the positive x-axis and along positive y-axis.

Solution:

x²/a² +y²/b² = 1                                       ...... (1)

According to the given condition the ellipse (1) passes through (3, 0) and (0, 2), so we have.

9/a² = 1 => a² = 9

And 4/b² = 1 => b² = 4

Therefore, the equation of the ellipse is x²/9 + y²/4 = 1

Illustration:

Obtain the equation of an ellipse whose focus is the point (-1, 1) whose directrix is the line passing through (2, 5) having the unit gradient and whose eccentricity is ½.

Solution:

Let P(x, y) be any point on ellipse.

Its focus is S (-1, 1).

Let the directrix be y = x + c                            ...... (1)

(·.· gradient m = 1)

Line (1) passes through (2, 5) so,

5 = 2 + c => c = 3

The directrix is y = x + 3

=> x - y + 3 = 0                                    ...... (2)

Now let PM be the perpendicular from P, drawn to its directrix

(2). By definition of ellipse SP = e PM

or SP² = e² PM²

=> (x + 1)² + (y - 1)² = (1/2)² [(x-y+3)/√((1²+1² ))]²

=> 8[(x + 1)² + (y - 1)²] = (x - y + 3)²

=> 7x² + 7y² + 2xy + 10x - 10y + 7 = 0,

This is the required equation of ellipse.

To read more, Buy study materials of Ellipse comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.