Applications of Gauss’s Law
Table of contents |
Applications of Gauss’s Law
Gauss’s Law can be used to solve complex electrostatic problems involving unique symmetries like cylindrical, spherical or planar symmetry. Also, there are some cases in which calculation of electric field is quite complex and involves tough integration. Gauss’s Law can be used to simplify evaluation of electric field in a simple way.
We apply Gauss’s Law in following way:
-
Choose a Gaussian surface, such that evaluation of electric field becomes easy
-
Make use of symmetry to make problems easier
-
Remember, it is not necessary that Gaussian surface to coincide with real surface that is, it can be inside or outside the Gaussian surface
Electric Field due to Infinite Wire
Consider an infinitely long wire with linear charge density λ and length L. To calculate electric field, we assume a cylindrical Gaussian surface due to the symmetry of wire. As the electric field E is radial in direction; flux through the end of the cylindrical surface will be zero, as electric field and area vector are perpendicular to each other. The only flowing electric flux will be through the curved Gaussian surface. As the electric field is perpendicular to every point of the curved surface, its magnitude will be constant.
Image 1: We consider a cylindrical Gaussian surface of radius r and length l
The surface area of the curved cylindrical surface will be 2πrl. The electric flux through the curve will be
E × 2πrl
and
According to Gauss’s Law
Vectorically, the above relation is
where 
is radial unit vector pointing the direction of electric field 
.
Image 2: Direction of Electric field is radially outward in case of positive linear charge density
Note 1: Direction of the electric field will be radially outward if linear charge density is positive and it will be radially inward if linear charge density is negative.
Note 2: We considered only the enclosed charge inside the Gaussian surface
Note 3: The assumption that the wire is infinitely long is important because, without this assumption, the electric field will not be perpendicular to the curved cylindrical Gaussian surface and will at some angle with the surface.
Electric Field due to Infinite Plate Sheet
Imagine an infinite plane sheet, with surface charge density σ and cross-sectional area A. The position of the infinite plane sheet is given in the figure below:
Image 3: Infinite Charge Sheet
The direction of the electric field due to infinite charge sheet will be perpendicular to the plane of the sheet. Let’s consider cylindrical Gaussian surface, whose axis is normal to the plane of the sheet. The electric field can be evaluated from Gauss’s Law as
According to Gauss’s Law:
From continuous charge distribution charge q will be σ A. Talking about net electric flux, we will consider electric flux only from the two ends of the assumed Gaussian surface. This is because the curved surface area and an electric field are normal to each other, thereby producing zero electric flux. So the net electric flux will be
Φ = EA – (– EA)
Φ = 2EA
Then we can write
The term A cancel out which means electric field due to infinite plane sheet is independent of cross section area A and equals to
In vector form, the above equation can be written as
whereis a unit vector depicting direction of electric field perpendicular and away from the infinite sheet.
Note 1: The direction of electric field is away from the infinite sheet if the surface charge density is positive and towards the infinite sheet if the surface charge density is negative.
Note 2: Electric field due to the infinite sheet is independent of its position.
Electric Field due thin Spherical Shell
Consider a thin spherical shell of surface charge density σ and radius “R”. By observation, it’s obvious that shell has spherical symmetry. The electric field due to the spherical shell can be evaluated in two different positions:
-
Electric Field Outside the Spherical Shell
-
Electric Field Inside the Spherical Shell
Electric Field Outside the Spherical Shell
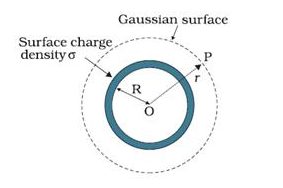
Image 4: Diagram of spherical shell with point P outside
To find electric field outside the spherical shell, we take a point P outside the shell at a distance r from the center of the spherical shell. By symmetry, we take Gaussian spherical surface with radius r and center O. The Gaussian surface will pass through P, and experience a constant electric field all around as all points is equally distanced “r’’ from the center of the sphere. Then,
According to Gauss’s Law
The enclosed charge inside the Gaussian surface q will be σ × 4 πR2. The total electric flux through the Gaussian surface will be
Φ = E × 4 πr2
Then by Gauss’s Law, we can write
Putting the value of surface charge density σ as q/4 πR2, we can rewrite the electric field as
In vector form, electric field is
where
is radius vector, depicting the direction of electric field.
Note: If the surface charge density σ is negative, the direction of the electric field will be radially inward.
Electric Field Inside the Spherical Shell
Image 5: Diagram of Spherical shell with point P inside
To evaluate electric field inside the spherical shell, let’s take a point P inside the spherical shell. By symmetry, we again take a spherical Gaussian surface passing through P, centered at O and with radius r. Now according to Gauss’s Law
The net electric flux will be E × 4 π r2. But the enclosed charge q will be zero, as we know that surface charge density is dispersed outside the surface, therefore there is no charge inside the spherical shell. Then by Gauss’s Law
Note: There is no electric field inside spherical shell because of absence of enclosed charge
Watch this Video for more reference
More Readings
Neet coaching| jee main preparation | online jee coaching in Delhi