Gauss’s Law
Table of contents |
Gauss’s Law
The Gauss Law, also known as Gauss theorem is a relation between an electric field with the distribution of charge in the system. The law was proposed by Joseph- Louis Lagrange in 1773 and later followed and formulated by Carl Friedrich Gauss in 1813.
Gauss’s Law states that the net electric flux is equal to 1/ ε0 times the charge enclosed in it. Mathematically Gauss Law is expressed as
where Φ is the net electric flux and q is the charge enclosed in it. The symbol
The integral form of electric flux is
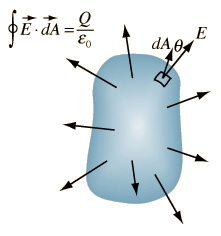
Image 1: Gauss’s Law
where E is the electric field flowing through small area element ds and q is the net charge enclosed in it. This form is used when we calculate electric flux in continuous charge distribution case. The surface, through which we calculate electric flux is called Gaussian Surface.
Example
There are three charges q1 = 3 C, q2 = 5 C and q3 = -2 C enclosed in a surface. What will be the total electric flux passing through the surface?
As according to Gauss’s Law, total electric flux equals 1/ ε0 times the total charge enclosed in a surface.
Total Charge = 3 C + 5 C – 2 C
Proof of Gauss’s Law
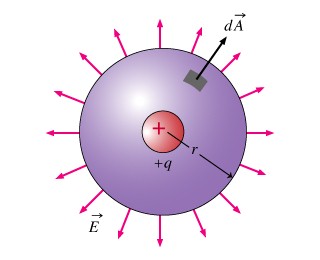
Consider a sphere of enclosed charge q inside it, placed at its center. The radius of the sphere is ‘r’. To prove Gauss’s Law, we need to find the net electric flux through the sphere. This can’t be done directly as the surface area is non-uniform in nature, otherwise we could have multiplied electric field with a surface area of the sphere. So, to evaluate electric field we will divide the sphere into small surface elements.
Image 2: Dividing a sphere into small surface area element dA
Now, each small surface area will feel same electric field due to charge q placed inside the sphere as each one is at equivalent distance ‘r’ from charge q. Adding further, these small surface elements will create small electric flux as
where kq/ r2 is the electric field produced by charge q on the small surface area element ds which is r distance away from it.
Is the direction vector, depicting the direction of electric field. As the direction of electric field and small surface area element is in the same direction that is, radially outwards, the small flux can be written as
The total electric flux of the sphere can be obtained by adding small flux through all the small surface area elements.
Since electric field on each surface area element is same, it will come out of the summation, that is,
The summation of all small area elements dA will give the total surface area A of the sphere that is 4πr2.
Note: The net electric flux through closed surface is zero, as there is no charge inside close surface.
Significance of Gauss’s Law
The most significant application of Gauss’s Law is that it is not only limited to simple cases but can be used in a general form. We consider following points while applying Gauss’s Law:
-
Gauss’s Law is always valid for any closed surface, irrespective of its shape that is, regular or irregular
-
We consider only the sum of charges which are present inside the closed surface
-
The inside charge and outside charge of the closed surface are responsible for electric field, but the electric flux will be due to inside charge only
Example
Suppose we take a Gaussian surface in such a way that there are inside and outside charges. Let’s say q1 is the inside charge and q2 is the outside charge, then the electric field will depend on both q1 and q2. However for the electric flux, while applying the Gauss’s Law we only consider the inside charge q1
-
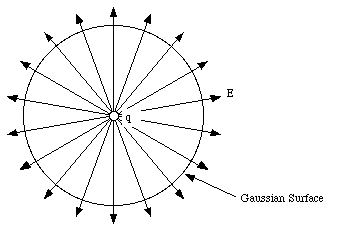
The closed surface is also called Gaussian Surface and we can assume Gaussian surface anywhere (even in continuous charge distribution system) except discrete charge, as Gaussian surface can’t pass through the discrete charge.
Image 3: Closed surface is also called Gaussian surface
-
Gauss’s Law can be used to make complex electrostatics problem simple with the help of symmetry
Image 4: Gauss’s Law can be used to evaluate electric flux in complex figures
-
Coulomb’s Law can be derived easily from Gauss’s Law, as both are inversely proportional to squared distance
Example
Consider three point charges –q, 2q, and 3q. The –q and 2q charge are enclosed in the surface, while the 3 q charge is outside the surface S. What is the net electric flux? Also, comment about the electric field. Refer the image below.
Image 5: Example of Net Electric Field
Solution:
According to Gauss’s law, we know that the net electric flux depends on the net charge enclosed in the surface. Therefore, we haven’t considered the charge + 3q as it was outside our Gaussian surface.
Net Charge enclosed in the surface = 2q – q = q
Electric flux Φ equals to
Considering about electric field, it will depend on all the three charges.
Watch this Video for more reference
More Readings