Circle
Table of Content |
|
|
History of Circles
 The circle has been come from the history as people observed the things like moon and sun as circle. The word circle was not the invention of one person but it was wheel, which when invented bring the properties of circle with it. The study of circle inspired the mathematicians to develop the concepts and properties related to circle.Rhynd papyrus bring the method of finding the method of calculating area of circle using and give its approximate value as 3.14. The book 3 of Euclid elements shows about the properties of circle. Then Plato gives the detailed explanation of circle in the Plato’s seventh letter.
The circle has been come from the history as people observed the things like moon and sun as circle. The word circle was not the invention of one person but it was wheel, which when invented bring the properties of circle with it. The study of circle inspired the mathematicians to develop the concepts and properties related to circle.Rhynd papyrus bring the method of finding the method of calculating area of circle using and give its approximate value as 3.14. The book 3 of Euclid elements shows about the properties of circle. Then Plato gives the detailed explanation of circle in the Plato’s seventh letter.
Meaning of Circle
A circle is a closed shape. It is a plane or you can say 2d shape. It is the set of all points which are at the same distance from a fixed point called Center.
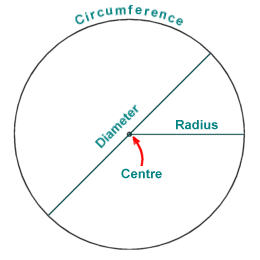
Parts of Circle
-
Center - The fixed point is center.
-
Radius - The distance between the fixed point (center) and any point on circle is called Radius. It is generally denoted by r.
-
Diameter - A longest line segment of the circle which passes through the center and which have two end points on the circle. All the diameters will have same length. It is the double of the radius that is, D=2r
-
Circumference - The circumference is the perimeter of the circle that is, the outline of the circle. It is calculated as 2r.
-
Chord - It is a line segment that has both the end points on the circle. Diameter is the longest chord. All the chords may have different length.
-
Arc - An arc is the two points on the circle which connect the circumference of the circle.
-
Tangent - It is a line which touches the circle at one point only. It is perpendicular to the radius at the point where it contacts the circle. That point is called the tangency point. As P in the above figure.
-
Segment – It is the area of the circle which comes inside the circumference of the circle and the chord, as shown above.
Inside and outside of the circle
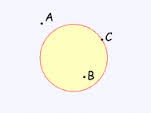
The points related to circle could be of three types-
-
Point inside the circle that is, point B.
-
Point outside the circle that is, point A.
-
Point on the circle that is, point C.
Properties of Circle
-
All circles are alike.
-
The circumference and the radius of the circle are proportional.
-
The circle which is has center points (0, 0) that is, at the origin of the plane and have a radius 1 is called unit circle.
-
The ratio of the circumference of the circle to the diameter is constant that is
Radius = r
Diameter = 2r
Area of Circle
It is the interior of the circle. It is calculated as
A = πr2
Where, A is the area of the circle and r is the radius of the circle.
Circle of Apollonius
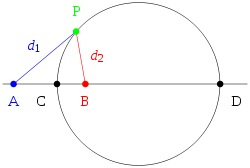
The definition of circle given by Apollonius is that the circle is a locus of all points in a plane that has a particular ratio of distances to the two fixed points called Foci.
Here, P is the point on the plane, A and B are the foci, d1 and d2 are the distances from P to foci A and B.
PC will bisect the angle APB, so the ratios of distances will same because of the angle bisector theorem.

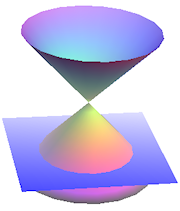
Circle in Conic Sections
A circle is one of the sections of a cone. When a plane intersects the right circular cone in such a way that the plane is perpendicular at the axis, or the plane is parallel to the base of the cone, or the angle of intersection of plane and the vertical axis is equal to 90° that is, ∅ = 90° , the surface comes out is circle. It is the special form of ellipse.
How many circles could be there in a cone?
As we move the plane upwards to the top, the circle become smaller and as we move the plane downwards, the circle turns to be bigger. There could be n number of circles in a cone with different radius.
Focus of Circle
Focus is a point from which the distance is measured to form conic. The circle has one focus point that is center of the circle.
Eccentricity of Circle
Eccentricity is the factor related to conic sections which shows how circular the conic section is. More eccentricity means less spherical and less eccentricity means more spherical. It is denoted by“e”.
The eccentricity of circle is 0 as it is closed and round shape.
Latus rectum of Circle
It is the line parallel to directrix and passes through focus. As the focus of the circle is center and the line passes through the center is diameter, the latus rectum of the circle is diameter of the circle.
Equation of Circle
- General form of equation of circle
Ax2 + Cy2 + Dx + Ey + F = 0
The expression B2 - 4AC is the discriminant which is used to determine the type of conic section represented by equation.
If equation fulfills these conditions, then it is a circle.
B2 - 4AC < 0, B = 0 and A = C
Example
Given equation is 4x2 + 4y2 -16x + 4y - 60 = 0, find whether it is the equation of circle or not?
Solution
Here A = 4, B = 0, C = 4
Determinant will be B2- 4AC
= 02-4(4) (4) = -64
This shows that B2 - 4AC < 0, B = 0 and A = C, so this is a circle.
In other way we can say that both variables are squared, and both squared terms are multiplied by the same number, so this is a circle
- Standard form of equation (Cartesian coordinates) of circle
Cartesian coordinates are the points on a plane with a pair of numerical coordinates which represented by (x, y).
- If the center is (0,0)
If the center of the circle lies on the origin of the plane, then the coordinates of the center of the circle (h, k) will be (0, 0). (x, y) are the coordinates of any point on the circle and r is the radius of the circle. So the equation will be-
x2 + y2 = r2
- If the center is (h,k)
If the center is not on the origin of the plane, then the equation will be-

where (h, k) are the coordinates of the center point and r is the radius of the circle.
Example 1
Find the equation of the circle with center (-2, 3) and radius 4.
Solution
Here, given, h = -3, k = 3 and r = 4
So the equation will be,
(x-3) 2+ (y + 3)2 = 16
Example 2
Find the center and radius of the circle x2 + y2 + 4x – 6y – 23 = 0
Solution
This equation can be written as
(x2 + 4x) + (y2 – 6y) = 23
Now we will complete the squares by adding 4 and 9 to the both sides.
x2 + 4x + 4 + y2 – 6y + 9 = 23 + 4 + 9 = 36
(x + 2)2 + (y - 3)2 = 36
So the center of the circle is (2.-3) and radius is 6.
Graph of Circle
To draw a graph of circle we must know the center of the circle. As we know the standard form of equation of circle is (x-h)2+(y-k)2=r2.This is also known as radius centered equation as it tells us about the coordinates of the center of the circle.
Here (h, k) is the center point of the circle, (x, y) is the point on the circle and r is the radius of the circle. The point h shows, how far it is from the center on y axis and k shows how far it is from the center on x axis. If we know the radius then we can count till r in all the four directions and plot the points to draw a circle.
- If the center is (0,0)
It is easy to draw a circle if its center is at the origin.
Example
Draw the graph of the circle with equation x2 + y2 = 9
Solution
Here we know that the (h, k) = (0, 0), so the center is at the origin. The radius is squared that is, 9 = 32 so radius is 3 that is, r = 3.
Now we will count till 3 in all the four directions so that we will get four points, then we will make the curve joining all the four points and we will get the circle for the equation.
- If the center is away from the origin
If we have to draw a circle which has its center away from the origin i.e. the center point must be something (h,k).Then we will plot the center at (h,k) then count till r in all the four direction s and draw a circle accordingly.
Example
Draw a graph of a circle with equation (x – 3)2 + (y +1)2 = 25
Solution
Here we know the center of the circle by the equation, (h, k) = (-3,1) and r = 5
So we will first plot the center of the circle on the graph we the coordinates (-3, 1). Then we will count till 5 on all the four directions from the center of the circle and plot the points accordingly. Now we can draw our circle easily.
Watch this Video for more reference
More Readings