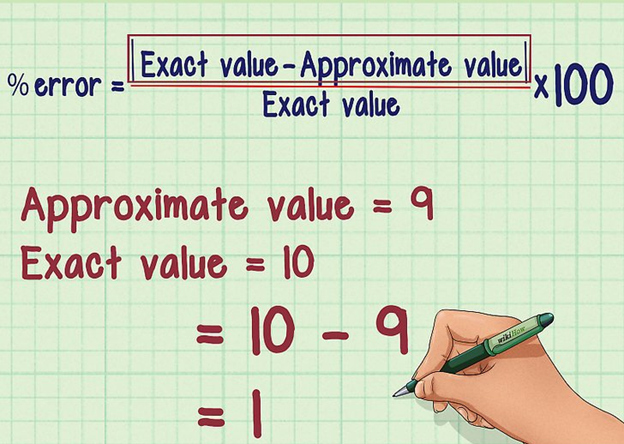IIT JEE Accuracy, Precision of Instruments and Errors in Measurements

 

Table of Content

Introduction to Error Accuracy Precision of Instruments Types of Error Systematic Errors Random Errors Least Count Error Absolute Error Relative Error Percentage Error Combination of Errors Error of a sum or difference Error of a product or quotient

Introduction to Error

Measurement is the basic requirement of almost every science experiment and theory. Be it studying about units and dimensions of a body or going through deep theories of electricity and magnetism, we need measurement in everything to understand the basic concepts behind it. Every measurement involves some form of uncertainty in the experiment.

For Example, Suppose you are measuring a building’s height in order to calculate the velocity of an object when it is thrown vertically upwards at a certain moment, and the instrument you’re using to measure the building is broken or defected, then your answer will definitely be wrong. The reason behind the wrong measurement is uncertainty in the instrument.

The uncertainties which occur while performing an experiment are called errors. Errors generally occur in the results of our experiments as every measured value has an error in it. It is very important to eradicate errors from our results so that it won’t create problems in future. The nature of the error is based on two terms, namely Accuracy and Precision.
 

Accuracy

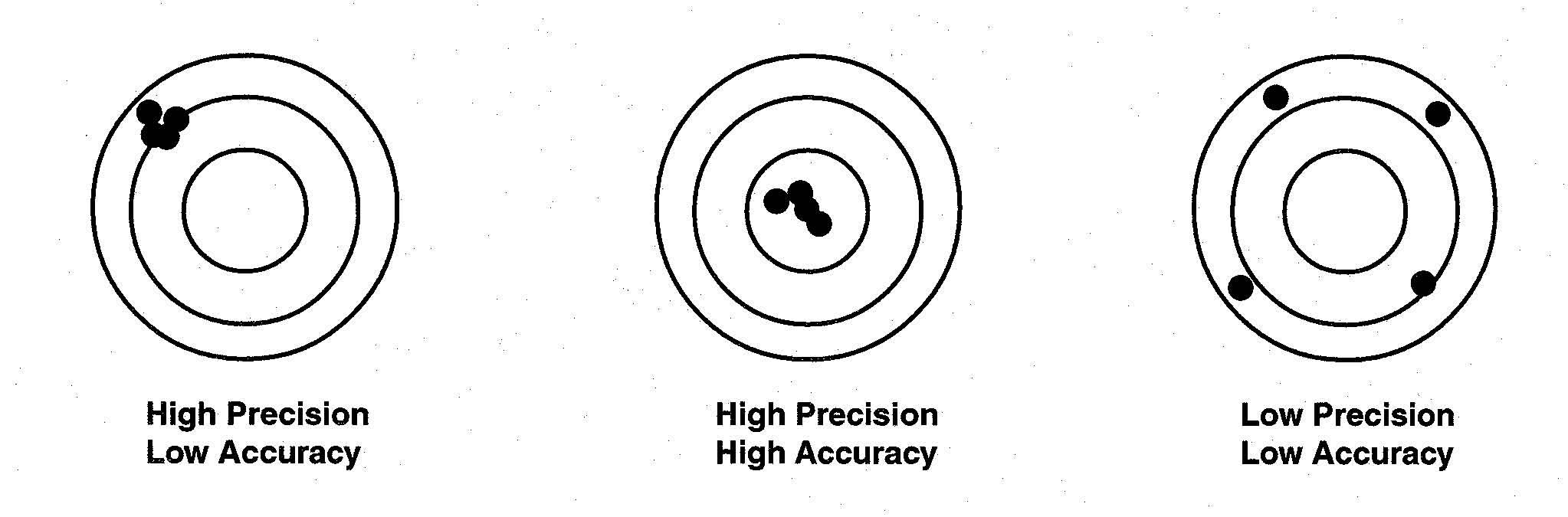
Image 1: Difference between precision and accuracy

Accuracy is defined as the closeness of measured value to a standard value. Suppose you weigh a box and noted 3.1 kg but its known value is 9 kg, then your measurement is not accurate.
 

Precision of Instruments

Image 2: Example depicting precision and accuracy

Precision is defined as the closeness between two or more measured values to each other. Suppose you weigh the same box five times and get close results like 3.1, 3.2, 3.22, 3.4, and 3.0 then your measurements are precise.

Remember: Accuracy and Precision are two independent terms. You can be very accurate but non-precise, or vice-versa.

Measurements of units revolve around accuracy and precision, that’s why we find our experiment readings to be in decimal form.
 

Types of Error

Image 3: Systematic error can occur in two ways

In a general manner, errors are basically of two types:

• Systematic Errors

• Random Errors

Systematic Errors

The errors which occur only in one direction are called Systematic Errors. The direction may be positive or negative but not be both at the same time. Systematic error is also known as a Repetitive Error as it occurs because of default machines and incorrect experiment apparatus.These errors take place if the device which is used to take measurements is wrongly calibrated. Some sources of systematic errors are as follows:

Instrumental Errors: The errors which occur due to lack of accuracy in an instrument are called instrumental errors. Instrumental Error occurs due to following reasons:

• If the instrument is not properly designed and is not accurate

• The calibration of the instrument is incorrect

• If the scale is worn off at edges or broken from somewhere

• If an instrument is giving a wrong reading instead of actual one

Examples

• If the markings of a thermometer are improperly calibrated, let’s say it’s 108°C instead of 100°C, then it is called An Instrumental Error

• If a meter scale is worn off at its end

• If pressure of atmosphere is 1 bar and the instrument is showing 1.5 bars, then it's again an instrumental error

• In a Vernier caliper, if the 0 of the main scale don’t coincide with that of Vernier scale then it is an instrumental error as the design of Vernier caliper is not proper

Imperfection in Technique: If the experiment is not performed under proper guidelines or physical conditions around are not constant, then this leads to imperfection in technique errors. These errors occur due to:

• If the instrument is not used properly

• If the instructions are not followed as per the rules of the experiment

• If environment is not well-suited with external physical conditions

• If the technique is not accurate

Example

• If we place thermometer under the armpit instead of the tongue, the temperature will always come out to be lower than that of body, as the technique of using thermometer is incorrect

Personal Errors: These errors occur due to improper setting of apparatus, lack of observation skills in an experiment and are based on the carelessness of individual only. Personal errors depend on the user or student performing the experiment and have nothing to do with instrument settings.

Example

• For measuring height of an object, if the student don’t place his head in a proper way, it may lead to parallax and readings won’t be correct

How to reduce systematic errors?

Systematic errors can be downplayed by:

• Improving experimental techniques by performing experiment as per the guidelines and precautions of the experiment

• By using correct, rightly accurate instruments and sending old worn out instruments for maintenance

• Concentrating more while performing an experiment in order to avoid silly mistakes in taking the readings of the measurement

• Removing personal mistakes as far as possible and keeping instruments safely after the experiment

Random Errors

Random Errors are not fixed on general perimeters and depend on measurements to measurements. That’s why they are named Random errors as they are random in nature. Random errors are also defined as fluctuations in statistical readings due to limitations of precisions in the instrument. Random errors occur due to:

• Sudden and unexpected shifts in experimental conditions of the environment

• Personal bias errors which even the student is unaware of

Example

• A spring balance will give different readings if the temperature of the environment is not constant

• If a person repeats an experiment he is more likely to get different observations

We can only reduce random errors and can’t eliminate them completely as they are unpredictable and not fixed in nature as systematic errors are.
 

Least Count Error

Image 4: All measuring instruments have least count on it.

The smallest value that can be measured in an instrument is called Least Count of the Instrument. Least count defines the main part of a measurement and occurs in both random as well as systematic Errors

Least Count Error depends on the resolution of the instrument. The Least Count Error can be calculated if we know the observations and least count of instruments. The table given below shows least count of some instruments.
 

Instrument	Least count
Vernier Caliper	0.01 cm
Spherometer	0.001 cm
Micrometer	0.0001 cm

We use high-precision instruments in order to improve experiment techniques, thereby reducing least count error. To reduce least count error, we perform the experiment several times and take arithmetic mean of all the observations. The mean value is always almost close to the actual value of the measurement.
 

Absolute Error

Absolute Error is defined as the difference between exact value and approximate value of respective readings. It tells how far a measurement from its true value is. As an example, suppose we perform an experiment in which readings are a₁, a₂, a₃, a₄, a₅ …. up to a_n and total number of observations is ‘n’,

Then mean value of measurement can be calculated as:

a_{mean =} a₁+a₂+a₃+………….+a_n/n

Absolute error is denoted by the notation |Δa| and errors in individual measurements can be calculated as:

Δa₁ = a_mean – a₁

Δa₂ = a_mean – a₂

Δa₃ = a_mean – a₃

_{…….       ………..      …}

Δa_n = a_mean – a_n

Remember that Δa may be a positive or negative sign, but will always focus on the magnitude of it. Also, the arithmetic mean of all absolute error is the final mean of absolute error of experiment.

Δa_mean = Δa₁ + Δa₂+ Δa_{3+……………..}+ Δa_n/n

Secondly, note that value of an always lies between a_mean - Δa_mean  and a_mean + Δa_mean. Mathematically the range of a measured value ‘a’ is

a_mean - Δa_mean  < a< a_mean + Δa_mean

In simple words Absolute Error  = Actual Value – Approximate value
 

Relative Error

Relative Error is defined as the ratio of the mean absolute error Δa_mean to the mean value a_mean of the quantity measured in an experiment. Instead of absolute error, we use relative error as it becomes easy to calculate errors and make necessary approximations.

Relative error = Δa_mean/ a_mean

Example

If the actual value of a quantity is 50 and its measured value is 49.8. Then calculate the absolute error and relative error in it.

We have a_mean = 50 (  a_mean and actual value are same thing)

Measured value = 49.8

Absolute error = Actual Value – Measured Value

= 50 – 49.8

= 0.2

Relative Error = 0.2/50 = 0.4%
 

Percentage Error

Image 5: Formulae to calculate percentage error

When we multiply relative error by 100, we get percentage error. Since the value of the relative error is very small it becomes convenient for us to write it in percentage. Mathematically,

Percentage Error = Relative Error × 100

Percentage Error = Δa_mean/ a_mean × 100
 

Combination of Errors

When we perform a physics experiment we have to deal with a number of errors involved. The errors can be in addition or subtraction form or may be in division or multiplication form. For Example, pressure is defined as force per unit area, and then if there is some error in force and area, there are chances that there will be an error in pressure too. Now how to calculate that error? There are two ways to calculate combined errors, they are:

• Error of a sum or difference

• Error in product or quotient

• Error in case of a measured quantity raised to a power

Error of a sum or difference

Let’s say two physical quantities A and B have actual values as A ± ΔA and B ± ΔB, then the error in their sum C can be calculated as

C = A + B, then maximum error in C will be

ΔC = ΔA + ΔB, for difference also follow the same formula. Remember that when two quantities are added or subtracted, the absolute error in the final answer will always be the sum of individual absolute errors.

Example

The length of two scales is given as l₁ = 20 cm ± 0.5 cm and l₂ = 30 cm ± 0.5 cm, then the final length by adding length of both scales will be given as 50cm  ± 1 cm

Error of a product or quotient

When two quantities are divided or multiplied, the relative error in the final answer is given as sum of relative error of each quantity

Suppose A and B are two quantities, with absolute error ΔA and ΔB and C is the product of A and B, that is, C = AB, then the relative error in C can be calculated as:

ΔC/C = ΔA/A + ΔB/B

Example

The mass of a substance is 100 ± 5 g and volume is 200 ± 10 cm³, then the relative error in density will be the sum of percentage error in mass that is  5/100 × 100 = 5% and percentage error in volume that is 10/200 ×100 = 5%, which is 10%.

Error in case of a measured quantity rose to some power

The relative error in physical quantity raised to a power‘s’ can be calculated by multiplying ‘s’ with a relative error of the physical quantity.

Suppose, there exist a quantity S = A², where A is any measured quantity, then relative error in S will be given as:

ΔS/S = 2ΔA/A

The general formula to find relative error in such cases can be written as:

Suppose S = A^xB^yC^z, , then

ΔS/S = x ΔA/A + y ΔB/B + z ΔC/C

Example

The relative error in S = A³B⁴C², will be written as,

ΔS/S = 3ΔA/A + 4ΔB/B + 2 ΔC/C

Watch this Video for more reference

More Readings

Accuracy, Precision of Instruments and Errors in Measurements