Mean-Life
Mean Life is an important topic of radioactivity. Just as the half-life of a radioactive substance is important, formula to calculate mean life is also equally important. The IIT JEE often picks up questions on the calculation of average life of radioactive substances. It is important to have expertise in this area as well in order to remain competitive in the JEE.
Mean life of radioactive elements is expected to be somewhat longer than the half-life. If in a given radioactive element, half of its elements have decayed after one half life, some well-defined average life expectancy can be assumed which is the mean life of the atoms.
Formulas of Calculating Radioactivity Mean Life
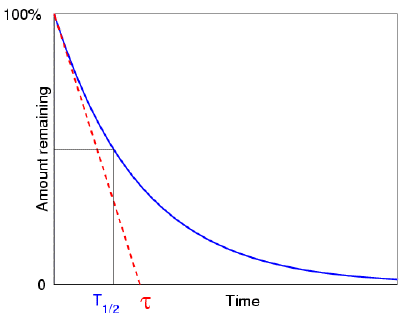
The mean life of an element equals the half-life of the substance divided by the natural logarithm of 2 which is about 0.693. In fact, the mean life turns out to equal the number τ which appears in the exponential term e−t/τ involved in the description of decay or growth. It is termed as the time constant.
Mean lifetime is a very significant quantity that can be measured directly for small number of atoms. If there are ‘n’ active nuclei, (atoms) (of the same type, of course), the mean life is
τ = τ
1 + τ3 + ... + τ2 / n
Where τ1, τ2,....... τn represent the observed lifetime of the individual nuclei and n is a very large number. It can also be calculated as a weighted average:
τ = τ1N1 + τ3N2 + ... + τ2Nn / N1 + ... + Nn
Where N1 nuclei live for time τ1,
N2 nuclei live for time τ2....... and so on.
This quantity may be related with γ.
Using calculus we may rewrite it as:
Where |dN| is the number of nuclei decaying between t, t + dt; the modulus sign is required to ensure that it is positive.
dN = –λN0e–λt dt
and |dN| = λN0e–λtdt


or τ = 1/λ.
The half-life and the mean life of substances are related to each other by the formula
T = τ ln 2 ≈ 0.693 τ
The two parameters vary drastically for different substances. For example the half-life of Polonium-212 is less than 1 microseconds, while for Thorium-232, the half-life crosses even 1 billion years.
Watch this Video for more reference
The JEE often asks questions on mean life equation or the average mean life of radioactivity. Let us consider one such proble
Illustration:
Cascade Decays: Frequently, a nucleus A decays into another nucleus B, which again decays into C, and so on until the series ends in a stable nuclide. These are known as cascade decays. We will consider a simple example of cascade decay where a nuclide A decays into B, and then, B decays into C:
λA λB
A ———> B ———> C
Suppose that there are N0 atoms of A to begin with. The problem is to find the numbers 0f atoms of A, B, C respectively as a function of time t.
Solution:
Suppose that at time t, there are NA atoms of A and Nb atoms of B. We write the equations:
dNA / dt –activity of A = –λANA … (i)
dNB / dt = + (activity of A) – (activity of B)
= λANA – λBNB … (ii)
Since each decay of A increases the number of atoms of B
dNC / dt = λBNB … (iii)
Solving equation (i), we get
NA (t) = N0 e–λA1 … (iv)
Substituting this in equation (ii), we get. the solution,
NB (t) =
 … (v)
… (v)
Putting the initial value (t = 0) of NB, we get C1, and substituting this value of C1 we get the expression for NB:
NB (t) =
 … (vi)
… (vi)
Substitution the value of NB in equation (iii) and solving, we get
NC =
 … (vii)
… (vii)
Using these values of NA, NB and NC, the activity can be calculated, if required
askIITians offers comprehensive study material containing numerous examples on calculation of mean life. The JEE aspirants can refer the notes for the use of mean life formula.
Related Resources
-
Click here for the Complete Syllabus of IIT JEE Physics.
-
Look into the Model Papers with Solutions to get a hint of the kinds of questions asked in the exam.
-
You can get the knowledge of Useful Books of Physics here.