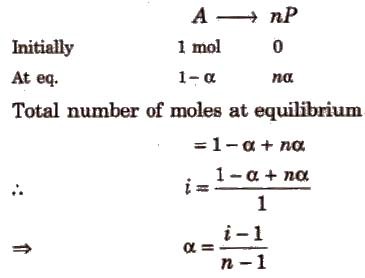Abnormal Molar Masses

 

Table of contents

Abnormal Molar Mass Association of Solute Particles Dissociation of Solute Particles Van’t Hoff Factor

Abnormal Molar Mass

Molecular masses of the solute can be easily determined with the help of colligative properties; relative lowering in vapour pressure, boiling point elevation, freezing point depression, and osmotic pressure easily. But, we derived the relation between the molecular mass of solute and colligative properties under some assumptions, which are:

• The solution is diluted that is, solvent is available in large amount in order to obey Raoult’s Law

• The solute neither went dissociation or association in the solution

So, how do we determine the molecular mass of solute in case the above assumptions are not valid? Basically, the abnormality is due to:

• Association of Solute Particles

• Dissociation of Solute Particles
   

Association of Solute Particles

Some solute molecules start to associate inside the solution. This means now there are less number of solute particles in the solution. As colligative properties vary with solute particles in the solution, they will decrease along with the solute particles. As colligative properties are inversely proportional to the molecular mass of solute, we get a higher molar mass of the solute. For Example, ethanoic acid or acetic acid ( CH₃COOH) associate in solution to form a dimer due to hydrogen bonding.
 

Dissociation of Solute Particles

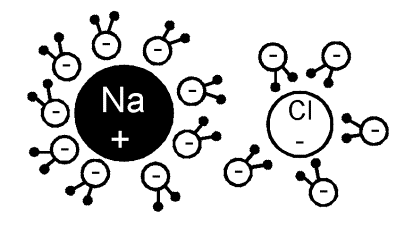
Some solute molecules, generally electrolytes dissociate into two or more ions/particles when dissolved in a solution. This leads to increase in solute particles in the solution, thereby increase in colligative properties of solutions. As colligative properties and molecular mass of solute varies inversely, we get a lower molar mass of the solute.

Image 1: NaCl dissociate into two ions when dissolved in water

Such a molar mass, whose value is higher or lower than its expected value is known as Abnormal Molar Mass. For Example, weak electrolytes dissociate in water to form ions, example Hydrofluoric Acid (HF), dissociate into hydrogen cation and fluorine anion.

Image 2: Ethanoic Acid dimerise due to hydrogen bonding

Van’t Hoff Factor

To determine colligative properties for solutions which undergo association and dissociation, a Dutch physical chemist Jacobus Henricus van’t Hoff in the year 1880 introduced the concept of Van’t Hoff Factor i to sort out association and dissociation problem while calculating the molar mass of solute.

The Van’t Hoff factor is denoted by ‘i’ and is obtained when we divide normal mass with an abnormal mass of solute. Mathematically, it is represented in three forms:

Calculation of i:

• First, we write an equation of the solute being associated or dissociated

• In case of dissociation, i = 1 + (n-1) α where n is number of particles dissociated and α is degree of dissociation

Image 3: Derivation of degree of association

• In case of association, i = 1 + (1/n – 1) α where n is the number of particles dissociated and α is degree of dissociation, the derivation is as follows:

• For solutes depicting Association, the Van’t Hoff factor is always less than 1, For Example when benzoic acid associates in benzene

• For solutes showing dissociation, the Van’t Hoff factor is always greater than 1, For Example, KCl and NaCl both have Van’t Hoff factor 2

• For particles showing neither dissociation or association, the Van’t Hoff Factor is taken as 1

The modified equations which can be used in the determination of molar mass in case of association or dissociation are as follows:

• Relative Lowering of Vapour pressure of Solvent,

where n₂ = moles of solute

n₁ = moles of solvent

= change in vapour pressure of solvent

P₁⁰ = vapour pressure of pure solvent

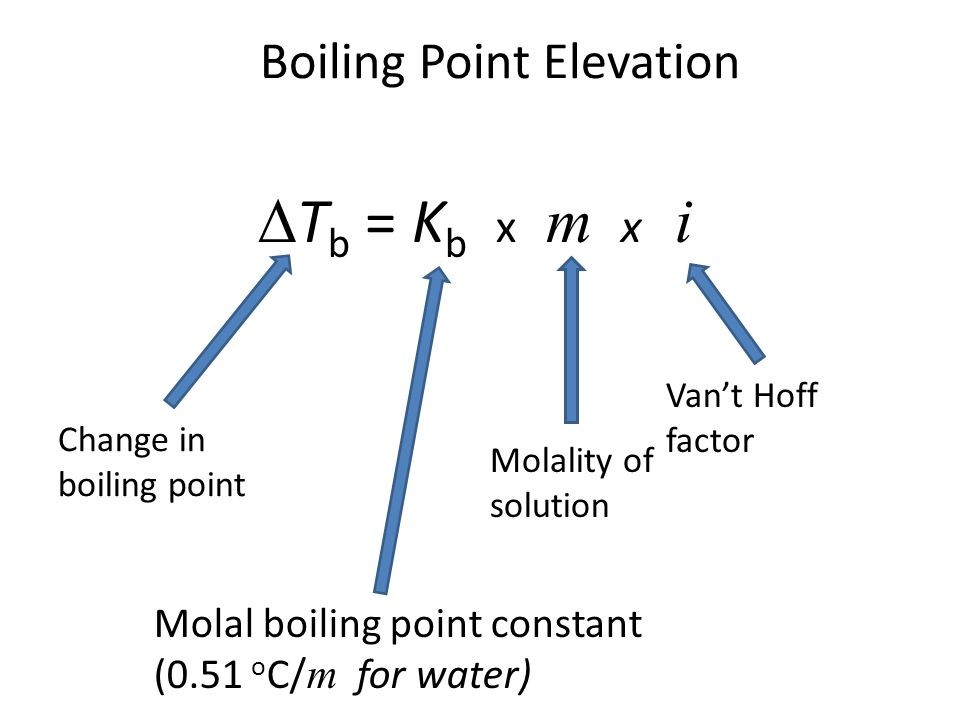
• Boiling Point Elevation, Δ T_b = i K_b m where K_b is elevation constant and m is molality of solute

Image 4: Elevation in boiling point relation

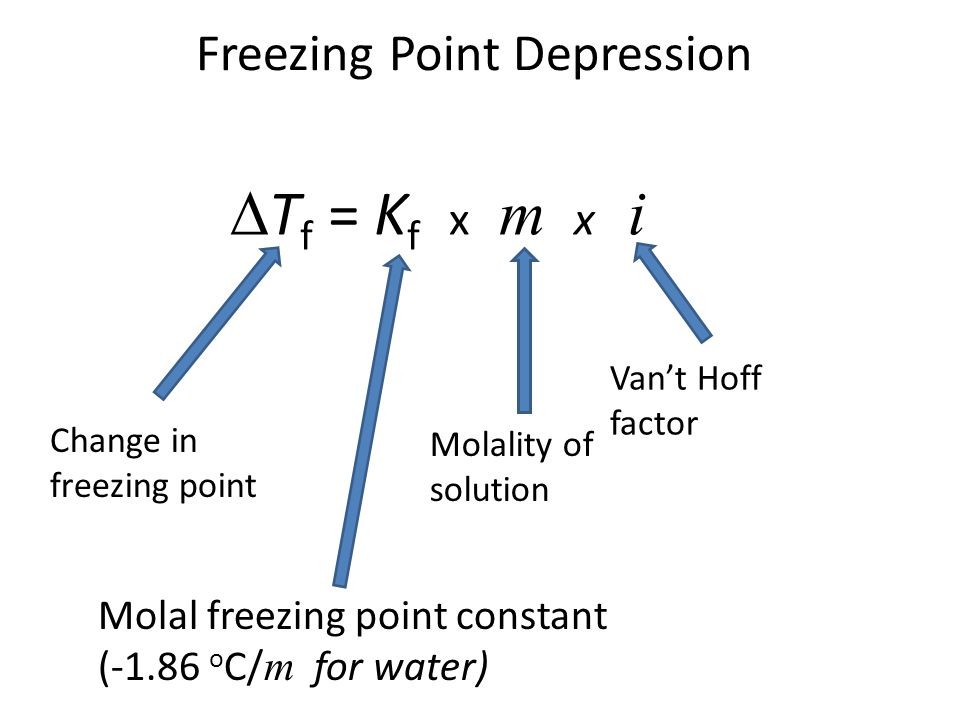
• Freezing Point Depression Δ T_f = i K_f m where K_f is depression constant and m is molality of solute

Image 5: Depression in freezing point relation

• Osmotic Pressure π = iCRT where C, R and T denotes concentration of solute, universal gas constant and temperature respectively

Example: The freezing point depression of an HF (aq) solution with molality 0.10 m is -0.201 C⁰. What will be the Van’t Hoff factor? Take the value of K_f to be 1.86 C⁰m^-1

The solution HF (aq) will dissociate as:

HF (aq) → H⁺ + F^-

We have Δ T_f = -0.201 C⁰ , m = 0.10 and K_f = 1.86 C⁰m^-1

The freezing point depression is Δ T_f = i K_f m

0.201 = i × 1.86 × 0.10

The value of Van’t Hoff factor will be 1.08

Watch this Video for more reference
 

More Readings

Abnormal Molar Masses