Representation of Points in a Plane

Table of Content

Representation of Points in a Plane
Locus of a Point
What is the meaning of an Equation of Locus?
- Procedure for finding the equation of the Locus of a Point
Length of the Perpendicular from a Point on a Line
- First Form
- Formula of Complete Distance
Related Resources

Coordinate Geometry is the unification of algebra and geometry in which algebra is used in the study of geometrical relations and the geometrical figures are represented by means of equations. The most popular coordinate system is the rectangular Cartesian system. Coordinates of a point are the real variables associated in an order to describe its location in space. Here we consider the space to be two-dimensional. Through a point O, referred to as the origin, we take two mutually perpendicular lines XOX’ and YOY’ and call them x and y axes respectively. The position of a point is completely determined with reference to these axes of means of an ordered pair of real numbers (x, y) called the coordinates of P where |x| and |y| are the distances of the point P from the y-axis and the x-axis respectively. X is called the x-coordinate or the abscissa of P and y is called the y-coordinate or the ordinate of P.

Representation of Points in a Plane

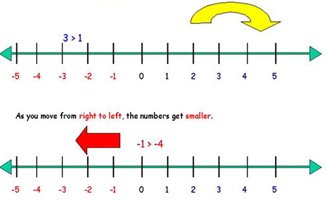
We are familiar with the representation of real numbers on a line, which we call a real line. In this representation we fix a point O (called origin) and represent a real number by a point A on this line such that its distance OA (see figure given below) is equal to the value of real number. The negative real numbers are represented in the left side of O while the positive real numbers are represented on the right side of the number line.

Thus, not only the magnitude, but the direction of the line is also taken into consideration for representation.

The figure given below illustrates that while the positive numbers are to the right of zero, the negative numbers lie on the left of zero.

Similarly ordered pairs are represented in a plane. To represent an ordered pair (a, b), we take two reference lines which are mutually perpendicular. The ordered pair (a, b) is represented in such a plane, by a point P(a, b) such that (see figure given below) OA = a and OB = b.

This system is called Cartesian co-ordinate system. Since elements of an ordered pair are not inter changeable (i.e., (a, b) ≠ (b, a) unless a = b) so they are represented in a particular order. The first element ‘a’ is represented on a horizontal line called abscissa and the second element ‘b’ on a vertical line called ordinate. Like the real number notation the positive side of the x-axis is the right side of O and positive side of O and positive side of y-axis is upper side of O.

So, the two lines divide the region in 4 parts. These are called quadrants. These quadrants are characterized as

I quadrant x > 0, y > 0

II quadrant x < 0, y > 0

III quadrant x < 0, y < 0

IV quadrant x > 0, y < 0

Here the point ‘O’ represents x = 0 and y = 0, hence order pair becomes (0, 0).

There is a second type of representation called the polar co-ordinate system. In this system a reference is fixed to a line (Called the initial line), and a point called the origin in the system. Any point P is represented by ordered pair (r, θ).

Such that

OP = r; The distance of point from origin.

and ∠POX = θ The angular displacement of line OP from fixed line i.e. the initial line, (in the anticlockwise direction)

Clearly ‘a’ = r cos θ and ‘b’ = r sin θ (see figure given below)

Locus of a Point

A locus of a point generally refers to a set of points satisfying a given condition. If a point moves according to some fixed rule, its co-ordinates will always satisfy some algebraic relation corresponding to the fixed rule. The resulting path (a curve) of the moving point is called the locus of the point. The locus i.e. the curve now contains all the points satisfying the specified condition and no point outside the curve satisfies the condition.

When a point moves in a plane under certain geometrical conditions, the point traces out a path. This path of the moving point is called its locus.

Eg: A circle is the locus of points on a plane that are at a certain distance from a central point. The figure given below illustrates the circle as the locus of points.

What is the meaning of an Equation of Locus?

The equation to the locus is the relation which exists between the coordinates of all the points on the path which holds true for no other points except those lying on the path.

Procedure for finding the equation of the Locus of a Point

If we are finding the equation of the locus of a point P, assign coordinates (h, k) or (x₁, y₁) to P.
Express the given conditions as equations in terms of the known quantities and unknown parameters.
Eliminate the parameters, so that the eliminant contains only h, k and known quantities.
Replace h by x, and k by y, in the eliminant. The resulting equation is the equation of the locus of p.

Length of the Perpendicular from a Point on a Line

The distance of a point from a line is the length of the perpendicular drawn from the point on the line. We know that the equation of a line can be written in different forms and so the length of the perpendicular can also be obtained in different forms.

First Form

The normal equation helps us in finding the distance of a point from a straight line. Suppose we have to find the distance of the point P(x₁, y₁) from the line l₁ whose equation is x cos α + y sin α = p. Let l₂ be the line through P parallel to the line l₁. Let d be the distance of P from l₁. Then, the normal from O to l₂ is of length p + d. Hence the equation of l₂ is

x cos α + y sin α = p + d.

Since P(x₁, y₁) lies on it.

∴ x₁ cos α + y₁ sin α = p + d

∴ d = x₁ cos α + y₁ sin α – p.

Note:

Rule to find the perpendicular distance of a given point from a given line in normal form:

If we have an equation whose right hand side is zero, then we can obtain the perpendicular distance by substituting the coordinates of the point in the left hand side of the equation. The result gives the perpendicular distance.

Formula of Complete Distance

If the point P and the origin O, instead of lying on the opposite sides of l as in figure given above, lie on the same side of line l₁ it may be proved by proceeding exactly in the same manner that

d = –(x₁ cos α + y₁ sin α – p)

Hence, the complete distance formula is

d = + (x₁ cos α + y₁ sin α – p)

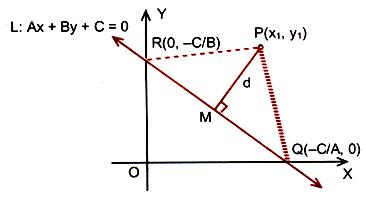
The distance of a point from a line is the length of the perpendicular drawn from the point to the line. Let L : Ax + By + C = 0 be a line, whose distance from the point P(x₁, y₁) is d. Draw a perpendicular PM from the point P to the line L. If the line meets the x and y-axes at the points Q and R respectively, then coordinates of the points are Q(–C/A, 0) and R(0, – C/B). Thus the area of the triangle PQR is given by

area(?PQR) = 1/2 PM × QR, which gives PM = 2 are (PQR)/QR … (1)

also, area (?PQR) = 1/2 |x₁ (0 + C/B) + (–C/A) (–C/B – y₁) + 0(y₁ – 0)|

= 1/2 |x₁ C/B + y₁ C/A + C²/AB|

Perpendicular PM from the point P to the line L

Or 2 area (?PQR) = |C/AB| |Ax₁ + By₁ + C| and

QR = √(0 + C/A)² + (C/B – 0)² = |C/AB| √A² + B²

Substituting the values of area (?PQR) and QR in (1), we get

PM = |Ax₁+ By₁+C|/√A²+ B².

Or d = |Ax₁+ By₁+ C|/√A²+ B².

Thus the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x₁, y₁) is given by d = |Ax₁+By₁+C|/√A²+ B².

Related Resources

Click here to refer the most Useful Books of Mathematics.
For getting an idea of the type of questions asked, refer the previous year papers.

To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.