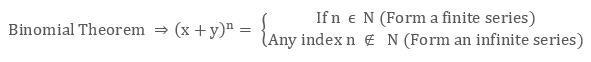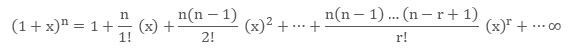Binomial Theorem
Table of Content |
Who developed the Binomial Theorem?
The journey of binomial started since the ancient times. Greek mathematician Euclid, in 4th century B.C, has given one of the special case of binomial theorem. Since then, many research work is going on and lot of advancement had been done till date. One of the biggest contributor in binomial theorem is considered as Persian mathematician Al-Karaji. He has explained the binomial coefficients with the triangular pattern. He also proved the binomial theorem and the pascal’s triangle.
What is the definition of Binomial in math? Explain Binomial Expression?
The word binomial is a special case of the word – “Polynomial”. Polynomial means an algebraic expression containing two or more algebraic terms. So, the binomial is also an algebraic expression containing exactly two different terms.
So, we can define binomial expression as an algebraic expression consisting of two different terms. Here, in its definition, the word different terms is very important to note. Different terms here means either the two terms should have different variables or the different powers on its variable.
Example
x + y, x2 + y3, x + x2 are the expression having two different terms and thus are categorized as binomial expression. Whereas, x + 2x or x2y + 2 x2y can be simplified into one terms and thus are not the example of binomial expression.
What is Binomial Theorem?
Binomial Theorem, in algebra, focuses on the expansion of exponents or powers on a binomial expression. This theorem was given by newton where he explains the expansion of (x + y)n for different values of n.
As per his theorem, the general term in the expansion of (x + y)n can be expressed in the form of pxqyr, where q and r are the non-negative integers and also satisfies q + r = n. Here, ‘p’ is called as the binomial coefficient.
What is (a + b)n?
In (a + b)n, a + b is the binomial and thus the expansion of (a + b)n can be easily calculated by the used of binomial theorem. But let’s here understand the binomial theorem from the basic level. Here, we will understand how the formula of binomial expansion is derived?

If we closely examine the expansion of (a + b) for different exponents, we observe that,
For (a + b)0 = 1
For (a + b)1 = a + b
For (a + b)2 = a2 + 2ab + b2
For (a + b)3 = a3 + 3a2b + 3ab2 + b3
For (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
From the above expansion, we can note few important properties of its expansion
-
The number of terms in the expansion of (a + b)n is n + 1 that is, if n = 3, the number of terms will be 3 + 1 = 4 and so on.
-
The power of a starts from n and decreases till it becomes 0.
-
Similarly, the power of b starts from 0 and increases till n
-
The binomial coefficients of the terms equidistant from the beginning and the end are equal. For Example, in (a + b)4 the binomial coefficient of a4 & b4, a3b & ab3 are equal
-
The sum of the powers of its variables on any term is equals to n.
-
The last and the very important conclusion which can be drawn is explained below with the help of figure.
The above triangle which you can see is called as the Pascal’s Triangle. This triangle represents the binomial coefficients for the expansion of different powers of (a + b).
The first row in the triangle represent the expansion of binomial theorem for the power zero. Similarly, the second row represent the binomials coefficient of the terms for the power one.
Pascals triangle is also very easy to understand and learn. Refer below figure to understand it.
From the figure, it is very clear that any number in the triangle is the addition of its upper two numbers.
Before generalizing the formula for the binomial expansion, just note that the binomials coefficients are nothing but the values of nCr for different values of r.
Thus, we can now generalize the binomial theorem for any non-negative power n.
(x + y)n = nC0xn + nC1xn-1y + nC2xn-2y2 + … + nCrxn-ryr + … + nCnxn-nyn.
From the above equation, we observe that
Second term, T2 = nC1xn-1y1
Third term, T3 = nC2xn-2y2
So the general term in the expansion of (x + y)n is
Tr+1 = nCrxn-ryr
How many terms in the expansion of (x + y + z + w)10 have?
Given problem is an expansion of quadrinomial or a polynomial having four terms. To understand the concept behind this problem, let’s go back to one of the very important property of binomial theorem. It says that, the sum of the powers of its variables on any term is equals to n, where n is the exponent on (x + y).
Thus, if we see the expansion of (x + y)n
(x + y)n = nC0xn + nC1xn-1y + nC2xn-2y2 + … + nCrxn-ryr + … + nCnxn-nyn.
Here, we can see that, the power n is being distributed to the variables x and y in every permutation. Thus, we can relate this distribution with the coin – beggar’s method of permutation and combination.
As per the coin – beggar’s method, the number of ways to distribute n identical coins to p beggar’s will be n + p -1Cp-1.
In our case, number of coins is the exponent of any polynomial and number of beggar’s is the number of terms in the polynomial.
Thus for (x + y + z + w)10, we have, n = 10 and p = 4
So, the number of terms in its expansion will be = 10+4–1C4-1 = 13C3
This method can also be verified for the binomial expansion, where we have n exponent and p = 2. So, the number of terms = n+1C1 = n+1 terms.
What is the binomial coefficient?
In (a + b)2 = 1a2 + 2ab + 1b2
1, 2 and 1 are called as the binomial coefficients of a2, ab and b2 respectively.
Similarly, in (a + b)3 = 1a3 + 3a2b + 3ab2 + 1b3
1, 3, 3 and 1 are called as the binomial coefficients of a3, a2b, ab2 and b3 respectively.
So, In general, in the expansion of (x + y)n
(x + y)n = nC0xn + nC1xn-1y + nC2xn-2y2 + … + nCrxn-ryr + … + nCnxn-nyn.
all the terms have a constant multiplied with the variables in the form of nCr. These nCr are called as the binomial coefficients of different terms (depending upon the value of r).
One more important point to note from here, is the sum of the binomial coefficients can be easily calculated just by replacing the variables to 1.
Example
The sum of the binomial coefficients of (x + y)n will be calculated as follows:
Put x = 1 and y = 1 in the expansion of (x + y)n, we get
(1 + 1)n = 2n = nC0 + nC1 + nC2 + … + nCr + … + nCn
How do you use Pascal's triangle?
Pascal’s triangle is named after the French mathematician Blaise Pascal. Pascal’s triangle is a triangular arrangement of binomial coefficients for the expansion of different powers.
Below is the pascal’s triangle for expansion till the exponent five.
This triangle can be expanded for any number of rows. Each row represents the binomial coefficient for any specific exponent.
For Example, the first and second row represent the binomial coefficients for the expansion of (x + y) with the exponent 0 and 1 respectively.
This triangle is also very easy to construct as each element in this triangle is the sum of upper two elements.
What is the binomial series?
Binomial series is a special series in mathematics, also called as the maclaurin series.
This series is a special case of the binomial theorem, where x = 1 and y = x
Binomial Series:
(1 + x)n = nC0 + nC1x + nC2x2 + …… nCrxr + …. + nCnxn

Depending upon the values of x and n, the series can be converging or diverging.
How to apply Binomial Theorem if n is negative or fractional?
The Binomial Theorem for the expansion of (x + y)n where n ∉ I+ will be expanded as,
So, the general term here will be,

Note: In this case, we can’t find the binomial coefficients using nCr directly, as this is not defined for negative n.
For (a + x)n where n ∉ I+,
In this case, where n is non positive integer, the series will converge only for (x/a) <1. But at the same time, the number of terms will be infinite i.e. infinite series.
Similarly for (1 + x)n where n ∉ I+,
Above series converges for |x| < 1
From the above series, we can get few important series which must be remembered as a formula.
-
(1 + x)-1 = 1 – x + x2 – x3 + x4 - ……..∞
-
(1 - x)-1 = 1 + x + x2 + x3 + x4 - ……..∞
-
(1 + x)-2 = 1 – 2x + 3x2 – 4x3 + 5x4 - ……..∞
How to find the term independent of x?
Term independent of ‘x’ here means that term in the binomial expansion which does not have any variable x involved in it.
Example
(x + y)2 = x2 + 2xy + y2, the third term that is, y2 is the term which is independent of ‘x’, while the first term that is, x2 is the term independent of y.
Example
(x + y)3 = x3 + 3x2y + 3xy2 + y3.
Here, the first term is independent of y and the fourth term is independent of x. Second and fourth terms involves both the variables x and y and thus are not independent of neither x or y.
Now, let’s learn – How to find the independent term in binomial expansion having any power.
Follow the below steps to find it:
-
For the given binomial with any power, write down its general term.
-
Combine all the ‘x’ terms using the laws of exponent (if not combine).
-
Equate the power or indices of ‘x’ to be zero to find the value of variable ‘r’.
-
After knowing r, if r is positive integer then (Tr+1)th term will be the term independent of x otherwise no such term exists.
If you just follow the above steps, you can easily find all such terms. See below example to understand the same.
Example
Which term is independent of x in the expansion of (x – x2)10
Step 1: Writing its general term,
Tr+1 = 10Crx10-r (-1)r(x2)r
Step 2: Now combining all the x terms,
Tr+1 = 10Crx10-r + 2r (-1)r = 10Crx10 + r (-1)r
Step 3: Equating the power of x to zero
10 + r = 0 that is, r = -10 which is not a positive integer.
Thus, no such term exists.
Example
Which term is independent of x in the expansion of (x – 1/x)20?
Step 1: Writing its general term,
Tr+1 = 20Crx20-r (-1)r(1/x)r
Step 2: Now combining all the x terms,
Tr+1 = 20Crx20-r - r (-1)r = 20Crx20 - 2r (-1)r
Step 3: Equating the power of x to zero
20 - 2r = 0 that is, r = 10 which is a positive integer.
Thus, r+1 = 11th term is independent of x.
This method is also helpful in finding any term or its coefficient having specific power of x. For example, in the example 4, if we are asked to find the coefficient of x15, we will solve as follows:
We have, Tr+1 = 10Crx10-r + 2r (-1)r = 10Crx10 + r (-1)r
For x15, we should equate the power of x to 15
that is, 10 + r = 15
thus, r = 5 that is, 6th term.
So, the coefficient = T6 = -10C5
More Readings