Revision Notes on Redox Reactions and Electrochemistry:

Electrochemistry is the branch of chemistry which deals with the chemical changes caused in the matter by passage of electric current and conversion of chemical energy into electrical energy and vice versa.

Conductors and Non Conductors

Substances around us can be divided into two classes based on their ability of conduct electricity:

Non-Conductors: Those substances which do not allow electric current to pass through them are called non-conductors or insulators. Example: - wood, plastic glass, rubber etc.
Conductors: Those substances which allow electric current to flow through tem are called conductors. Examples: Copper, Iron, Gold, Silver, Graphite, salt solution etc.

Conductors can further be divided into two groups

Metallic Conductors: These conductors conduct electricity or electric current by movement of electrons without undergoing any chemical change during the process. These conduct electricity in both solid as well as molten state. Example: All the metals and Graphite
Electrolytes: Those substances which conduct electricity only when they are present in aqueous solution and not in solid form are called electrolytes. These conduct electricity by movement of ions in solutions.

Comparison of Electrolytic and Metallic Conduction

S.No	Metallic Conduction	Electrolytic Conduction
1	Electric current flows by movement of electrons.	Electric current flows by movement of ions.
2	No chemical change occurs.	Ions are oxidized or reduced at the electrodes.
3	It does not involve the transfer of any matter.	It involves transfer of matter in the form of ions.
4	Ohm's law is followed.	Ohm's low is followed.
5	Resistance increases with increase of temperature.	Resistance decreases with increase of temperature.
6	Faraday law is not followed.	6Faraday law is followed.

Electrolytic Conductance:

Specific Resistance or resistivity (ρ):

R = ρ× l /A

Where,

R = Resistance

A=Area of cross sections of electrodes

l = Distance between the electrodes.

Specific Conductance or Conductivity (κ):

κ = 1/ ρ

Units: W^–1 cm^–1 or Sm^–1

Equivalent Conductance (Λ):

Conducting power of all the ions produced by one g-equivalent i.e. one equivalent of an electrolyte in a given solution

Λ = 1000 κ /C

Where, C be the normality of solution i.e. concentration of electrolytic solution in equivalent/L.

Units: W^–1cm²

Molar Conductance (Λ_m):

Conductance of solution due to all the ions produced by one mole of the dissolved electrolyte in a given solution.

Λ_m= κ/c

Where, c = concentration of solution in mol m^-3.

Λ_m= κ×1000/M

Where, M is molarity of solution.

Units: S cm² mol^-1

Relation between Λ and Λ_m

Λ_m = n Λ

Where n = n-factor of the electrolyte = total charge carried by either ion = M/E

Variation of Conductance with Dilution:

Specific conductance: Decrease with dilution due to decrease in number of ions per c.c. of the solution.

Molar and Equivalent Conductance: Increases with increase in dilution.

Weak electrolyte: Increase is due to increase in extent of ionization.
Strong electrolyte: Increase is due to increase in mobility of ions because of decreased inter-ionic attraction.

Debye-Hückel-Onsager Equation

Λ_{m =}Λ⁰_m–(A+B Λ⁰_m) √C

Where,

A & B = Debye-Hückel constants.

C = Molar concentration

Λ⁰_m= Limiting molar conductivity i.e. molar conductivity at infinite dilution.

At 298 K,

Λ_{m =}Λ⁰_m–(60.2 – 0.299 Λ⁰_m) √C

Kohlransch’s Law of Independent Migration of Ions:

"At infinite dilution, when dissociation is complete, each ion makes a definite contribution towards equivalent conductance of the electrolyte irrespective of the nature of the ion with which it Is associated and the value of equivalent conductance at infinite dilution for any electrolyte is the sum of contribution of its constituent ions", i.e., anions and cations. Thus,

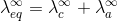
where,

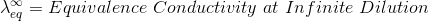
$\lambda^\infty _e_q =Equivalence\ Conductivity\ at\ Infinite\ Dilution$

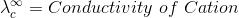
$\lambda^\infty _c =Conductivity\ of\ Cation$

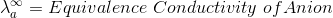
$\lambda^\infty _a =Equivalence\ Conductivity\ of Anion$

According to Kohlrausch’slaw. “conductivity of ions is constant at infinite dilution and it does not depend on nature of co-ions.”

For A_xB_y type electrolyte,

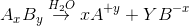
$A_xB_y \overset{H_2O}{\rightarrow} xA^+^y +YB^-^x$

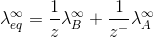
$\lambda ^\infty _e_q = \frac{1}{z}\lambda ^\infty _B +\frac{1}{z^-}\lambda ^\infty _A$

Here Z⁺and Z^- are the charges present on cation and anion.

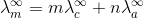
$\lambda ^\infty _m = m\lambda ^\infty _c +n\lambda ^\infty _a$

Here m and n are the number of moles of cations and anions.

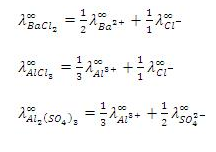
Faraday’s Laws of Electrolysis:

First Law: “The mass of a substance deposited or liberated at any electrode is directly proportional to the amount of charge passed.”

w = zQ

Where z = electrochemical equivalent i.e. the mass of the substance in grams deposited or liberated by passing one coulomb of charge,

Second Law: “Mass of a substance deposited or liberated at any electrode on passing a certain amount of charge is directly proportional to its chemical equivalent weight”.

Charge on one mole electrons = 1 F = 96487 C

That is w a E where w is the mass of the substance in grams while E is its chemical equivalent weight in gms per equivalent=

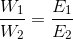$\frac{W_1}{W_2}=\frac{E_1}{E_2}$ .

The charge possessed by 1 mole of electrons

= 1.6 $\times$ 10^–19 $\times$ 6.023 x 10²³ ≈ 96500 C

This charge is called as 1 Faraday.

If we pass one Faraday of charge, it means that we are passing one mole of electron and by passing 1 Faraday of charge 1gm equivalent weight of the substance will be deposited or liberated.

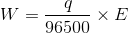
$W=\frac{q}{96500}\times E$

By combining the first and second law, we get

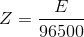
$Z=\frac{E}{96500}$

Electrochemical Cells:

Difference in Electrolytic Cell and Galvanic Cell:

Electrolytic Cell	Galvanic cell
Electrical energy is converted into chemical energy.	Chemical energy is converted into electrical energy.
Anode positive electrode. Cathode negative electrode	Anode negative electrode. Cathode positive electrode.
Ions are discharged on both the electrodes.	Ions are discharged only on the cathode
If the electrodes are inert, concentration of the electrolyte decreases when the electric current is circulated	Concentration of the anodic half-cell increases while that of cathodic half-cell decreases when the two electrodes are joined by a wire
Both the electrodes can be fitted in the same compartment	The electrodes are fitted in different compartment

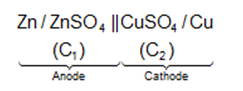
Standard electrode potential: The potential difference developed between metal electrode and the solution of its ions of unit molarity (1M) at 25°C (298 K)

IUPAC Cell Representation: Anode (Molarity of electrolyte at anode) || Cathode (Molarity of electrolyte at cathode)

E⁰_cell= E⁰_cathode- E⁰_anode

Example:

The Nernst Equation:

For a general reaction such as

M₁A + m₂B ..... n₁X + n₂Y + .... .......(i)

Occurring in the cell, the Gibbs free energy change is given by the equation

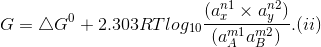
$G = \bigtriangleup G^0 + 2.303RT log_1_0\frac{(a_x^n^1 \times a_y^n^2)}{(a_A^m^1 × a_B^m^2) } ...(ii)$

where

'a' represents the activities of reactants and products under a given set of conditions and

?G^o refers to free energy change for the reaction when the various reactants and products are present at standard conditions.

The free energy change of a cell reaction is related to the electrical work that can be obtained from the cell, i.e.,

?G^o = -nFE_cell and ?G^o = -nFE^o.

On substituting these values in Eq. (ii) we get

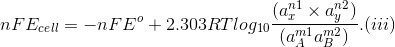
$nFE_c_e_l_l = -nFE^o + 2.303RT log_1_0\frac{(a_x^n^1 \times a_y^n^2)}{(a_A^m^1 × a_B^m^2) } ....... (iii)$

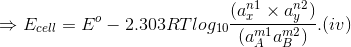
$\Rightarrow E_c_e_l_l = E^o - 2.303RT log_1_0\frac{(a_x^n^1 \times a_y^n^2)}{(a_A^m^1 × a_B^m^2) } ....... (iv)$

This equation is known as Nearnst equation.

Some other important relations:

K_eq = e^nE/FRT
ΔH = nF [T(dE/dT)-E]
ΔS = nF(dE/dT)_P

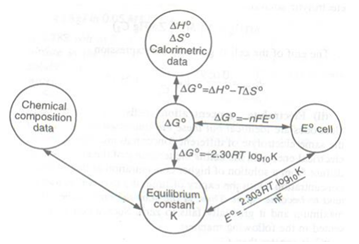
Some Important Half Cells:

Hydrogen Electrode:

The electrode reaction : H₂ -> 2H⁺ + 2e^–
Electrode representation: Pt | H₂ (1 atm) | H⁺ (1M).

Ferrous – Ferric Electrode:

Electrode reaction: Fe³⁺ + e^– -> Fe²⁺
Electrode representation: Pt | Fe²⁺ (C₁), Fe³⁺ (C₂).

Quin – Hydrone Electrode:

Electrode reaction:
Electrode representation: Pt.|QH₂,Q,H⁺ (C)

Calomel electrode :

Electrode reaction : ½ Hg₂Cl₂+e^- ↔ Hg +Cl^-
Electrode is representation: Cl^- (1M) | Hg₂Cl₂, Hg?

?Oxidation and Reduction

Oxidation is defined as the loss of electrons by a chemical species (atom, ion or molecule).
Reduction is the gain of electrons by a chemical species (atom, ion or molecule).
An oxidising agent that chemical species which takes electrons thus it is an electron acceptor.
A reducing agent is the chemical species that gives electrons and thus acts as an electron donor.
When Fe²⁺(aq) ions are being oxidised they are acting as reducing agents, and when Fe³⁺(aq) ions are being reduced they are acting as oxidising agents. In general ;

Neither reduction nor oxidation occurs alone. Both of them occur simultaneously. Since both these reactions must occur at the same time they are often termed as "redox reactions". The oxidation or reduction portion of a redox reaction, including the electrons gained or lost can be determined by means of a Half-Reaction

?Oxidation Number

The oxidation number for an element in a covalent compound is by taking the oxidation number to be equal to the charge that the element would carry, if all the bonds in the compound were regarded as ionic instead of covalent.
The sum of the oxidation numbers of all the atoms in an uncharged compound is zero. In case of an ion, the algebraic sum of the oxidation numbers of all the atoms is equal to the charge on the ion.
Oxidation number of any element in its elementary state is zero.
Fluorine is the most electronegative element. Its oxidation number is always -1 .
Oxygen after fluorine is the second most electronegative element. It shows an oxidation state of -2 in almost all the compounds excepts peroxides and superoxides,
In all compounds, except ionic metallic hydrides, the oxidation number of hydrogen is +1.
In any compounds has more than two elements, the oxidation number of any one of them may have to be obtained by first assigning reasonable oxidation numbers to the other elements.

Oxidation Number / State Method For Balancing Redox Reactions:

This method is based on the principle that the number of electrons lost in oxidation must be equal to the number of electrons gained in reduction. The steps to be followed are :

Write the equation (if it is not complete, then complete it) representing the chemical changes.
By knowing oxidation numbers of elements, identify which atom(s) is(are) undergoing oxidation and reduction. Write down separate equations for oxidation and reduction.
Add respective electrons on the right of oxidation reaction and on the left of reduction reaction. Care must be taken to ensure that the net charge on both the sides of the equation is same.
Multiply the oxidation and reduction reactions by suitable numbers to make the number of electrons lost in oxidation reactions equal to the number of electrons gained in reduction reactions.
Transfer the coefficient of the oxidizing and reducing agents and their products to the main equation.
By inspection, arrive at the co-efficients of the species not undergoing oxidation or reduction.
Some elements like manganese, chromium, nitrogen and chlorine show variable oxidation states.
When an element is oxidised its oxidation number gets increased while reduction on any element decreases its oxidation number. Change in oxidation number can be used to decide whether an oxidation or a reduction has taken place. In the change from chloromethane to dichloromethane, for example,
C H₃ Cl C H₂ Cl₂
-2 +1 -1 0 +1 -1
The oxidation number of carbon is increased from -2 to 0. The carbon is therefore being oxidised.

Half-Reaction or Ion-Electron Method For Balancing Redox Reactions

This method involves the following steps :

Divide the complete equation into two half reactions, one representing oxidation and the other reduction.
Balance the atoms in each half reaction separately according to the following steps:
- First of all balance the atoms other than H and O.
- In a reaction taking place in acidic or neutral medium, oxygen atoms are balanced by adding molecules of water to the side deficient in oxygen atoms while hydrogen atoms are balanced by adding H⁺ ions to the other side deficient in hydrogen atoms. On the other hand, in alkaline medium (OH^-), every excess of oxygen atom on one side is balanced by adding one H₂O to the same side and 2OH^- to the other side. In case hydrogen is still unbalanced, then balance by adding one OH^-, for every excess of H atom on the same side as the excess and one H₂O on the other side.
- Equalize the charge on both sides by adding a suitable number of electrons to the side deficient in negative charge.
- Multiply the two half reactions by suitable integers so that the total number of electrons gained in one half reaction is equal to the number of electrons lost in the other half reaction.

Common Oxidising and Reducing Agents

Oxidising agent	Effective Change	Decrease in Oxidation Number
KMnO₄ in acid solution	MnO₄^- → Mn²⁺	5
KMnO₄ in alkaline solution	MnO₄ ^-→ MnO₂	3
K₂Cr₂O₇ in acid solution	Cr₂O₇^2- → Cr³⁺	3
dilute HNO₃	NO₃^- → NO	3
concentrated HNO₃	NO₃^- → NO₂	1
concentrated H₂SO₄	SO₄^2-→ SO₂	2
manganese (IV) oxide	MnO₂ → Mn²⁺	2
chlorine	Cl → Cl^-	1
chloric (I) acid	ClO^- → Cl^-	2
KlO₃ in dilute acid	IO₃^- → I	5
KlO₃ in concentrated acid	IO₃^- → I^-	4
Reducing agent	Effective Change	Increase in Oxidation Number
iron (II) salts (acid)	Fe²⁺ → Fe³⁺	1
tin (II) salts (acid)`	Sn²⁺ → Sn⁴⁺	2
ethanedioates (acid)	C₂O₄^2- → CO₂	1
sulphites (acid)	SO₃^2- →SO₄^2-	2
hydrogen sulphide	S^2- → S	2
iodides (dilute acid)	I^- → I	1
iodides (concentrated acid)	I^- → I⁺	2
metals, e.g. Zn	Zn → Zn²⁺	2
hydrogen

Live courses Ask question