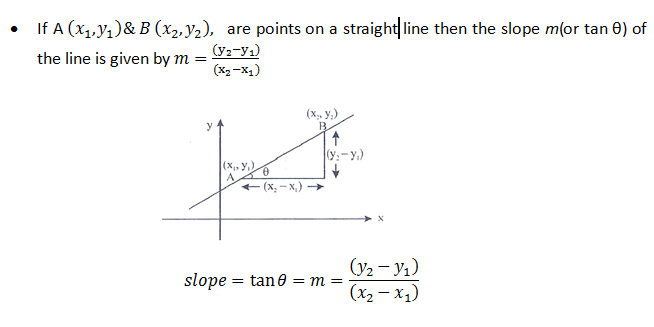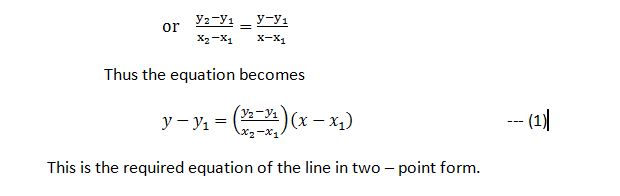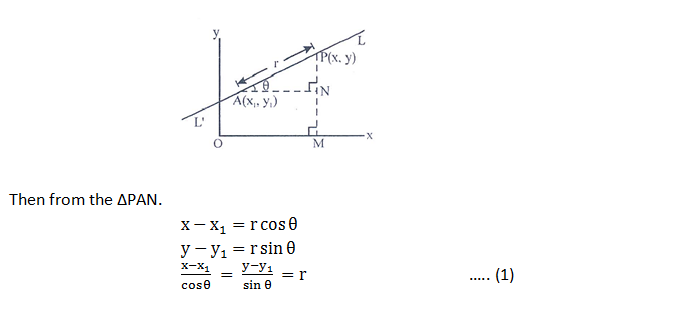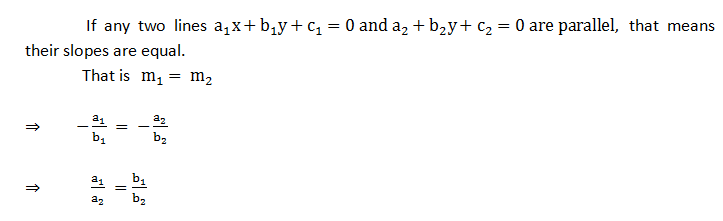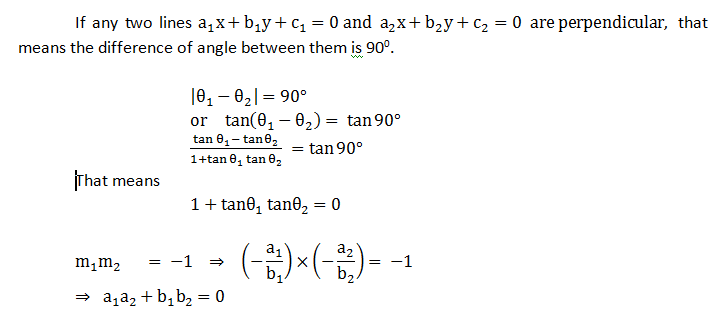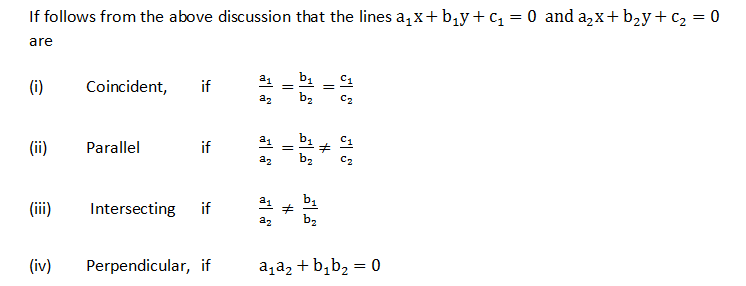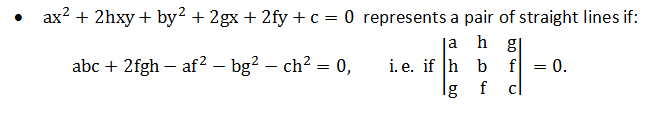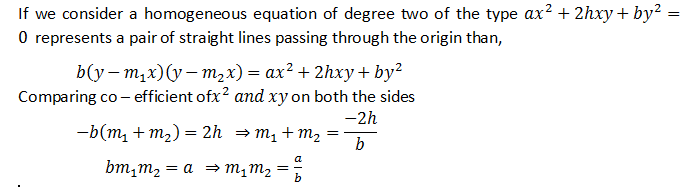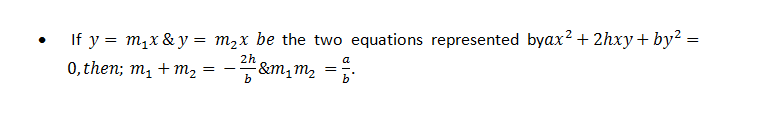Straight forward tricks and concepts for the STRAIGHT LINE

After reading this article, students will be able to understand the concepts of straight line from basic level up to the advanced level. Understanding the concept of straight line is important as this forms the basis of 2D and 3D geometry. We will try to look the straight line in a very simple way in this article and thus will help you in understanding it clearly.

LOCUS: The term Locus is most frequently used in the co-ordinate geometry. It is defined as the curve described by a point which moves under given condition(s). The equation of the locus of a point means the equation satisfying co-ordinates of every point.

Follow the below given steps to find the equation of locus of a point:

Step I Assume the coordinates of the point say (h,k) whose locus is to be found.

Step II Write the given condition in mathematical form involving h, k.

Step III Eliminate the variable(s), if any.

Step IV Replace h by x and k by y in the result obtained in step III. The equation so obtained is the locus of the point, which moves under some stated condition(s).

STRAIGHT LINEis a locus of the point P (h,k) which moves in such a way that point P is collinear with the two given points. We can also define straight line as a curve such that the every point on the line segment joining any two points on it lies on it. Line is a 1-D curve and thus its equation will be of degree one.

• For 0< θ < Ï€/2 :- Slope is positive (since tan is positive in first quadrant)
• For Ï€/2 < θ <Ï€ :- Slope is negative (since tan is negative in second quadrant)

 If we consider a single point, definitely infinite numbers of straight lines can be drawn passing through it. But if we are given two points, then one and only one line passes through it. Thus we require at least two conditions to get one unique line. Depending upon the two conditions available with us, we can write the equations in different forms. Some of them are:

A.   TWO-POINT FORM OF A LINE:

Consider two points A(x₁, y₁) and B(x₂, y₂). Let C(x,y) be any point which is collinear with A and B (condition for any point to be on a line). Thus we can say, slope of AB = slope of AC

C. SLOPE-INTERCEPT FORM OF A LINE:

Now consider the equation obtained in (2) and assume that this line passes through (0,c) on the y – axis.

Thus we can replace (x₁, y₁) by (0,c). The equation will become

y-c = mx

or y = mx + c

where c is called the y intercept of the line.

This is the required equation of the line in slope- intercept form.

D. INTERCEPT FORM OF A LINE:

In this form of equation of line, we will be given with the x and y intercept. So we can easily get the co-ordinates of the points of line on x and y axis respectively.

If x-intercept is a, that means line passes through (a,0) on the x-axis. Similarly, if y-intercept is b, that means line passes through (0,b) on the y – axis. Using these two points, we can easily write the equation of line as,

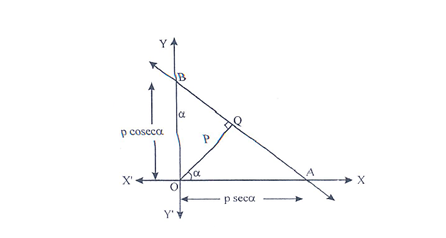
E. NORMAL FORM OR PERPENDICULAR FORM OF A LINE:

In this form of the straight line, the length of perpendicular from the origin and an angle which this perpendicular makes with positive direction of x-axis is known to us.

Let AB be the line such that the length of the perpendicular OQ from the origin O to the line be p and ∠ XOQ = α.

From the diagram, we can easily find the length OA and OB using trigonometric ratios.

Thus OA = p sec α and OB = p cosec α

These OA and OB are actually the x and y intercepts of the line AB.

Thus using intercept form, we can write,

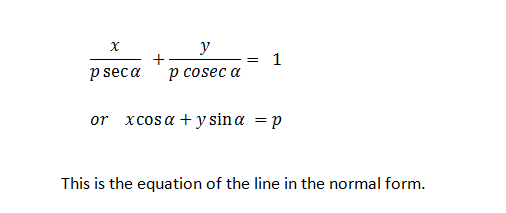F.  PARAMETRIC FORM OF A LINE:

In this form of equation of a line, a point and its inclination with the positive direction of x –axis (in anticlockwise direction) is known to us. By knowing the inclination angle, we can also find the slope but sometimes writing the equation in terms of ‘theta’ as a new parameter simplifies the given problem. Therefore we go for this form of a line.

Let’s now analysis the situation and derive the equation of line in parametric form.
Consider a point P (x, y) taken on the line above the given point (x₁, y₁)

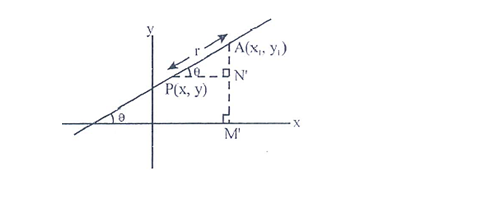
Again, if consider a point is taken on the line below the given point A (x₁, y₁), then from the ∆APN’

• CONDITION FOR THE LINES TO BE PARALLEL:

• CONDITION FOR THE LINES TO BE PERPENDICULAR: 

• WRITING AN EQUATION OF ALINE PARALLEL TO A GIVEN LINE:

Any line parallel to a given line will have the same slope but different intercept. So the equation of a line parallel to a given line ax + by + c = 0 is
Where λ is a constant and value of λ can be determined using another given condition.

• WRITING AN EQUATION OF ALINE PARALLEL TO A GIVEN LINE:

Any line parallel to a given line will have the same slope but different intercept. So the equation of a line parallel to a given line ax + by + c = 0 is                            Where λ is a constant and value of λ can be determined using another given condition.

• PAIR OF STRAIGHT LINES: 

In this section we will discuss about the combined equation of two lines. When any two line Intersects at a point, than we can write  a single equation representing the two lines. The angle θ between the two lines represented by a general equation is the same as that between the two lines represented by its homogeneous part only.

• GENERAL EQUATION OF SECOND DEGREE REPRESENTING A PAIR OF STRAIGHT LINES:

• A PAIR OF STRAIGTH LINES THROUGH ORIGIN:

Pair of straight lines through origin means origin is the common point of intersection and thus point O (0, 0) will satisfy any general equation of pair of straight line.

Note:  A homogeneous equation of degree n represents n straight lines through the origin.

I am Vijay Mukati, Mathematics Expert at askIITians. I did my post-graduation from IIT Patna. For more about me you can visit the following link

You can also refer to some of my Video Lectures in Physics, available on the following links.

Communication System

Semiconductor Devices

Wish you all the best. For any queries please do ask us or you can post any question on our free forum.