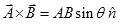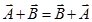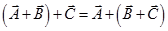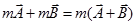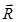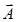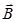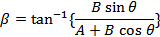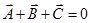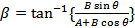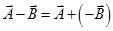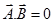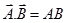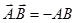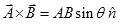The three equations of motion for an object with constant acceleration are given below. 
(a) v= u+at
(b) s= ut+1/2 at2
(c) v2=u2+2as
Here u is the initial velocity, v is the final velocity, a is the acceleration , s is the displacement travelled by the body and t is the time.
Note: Take ‘+ve’ sign for a when the body accelerates and takes ‘–ve’ sign when the body decelerates.
	
The displacement by the body in nth second is given by,
sn= u + a/2 (2n-1)
	
Position-time (x vs t), velocity-time (v vs t) and acceleration-time (a vs t) graph for motion in one-dimension: 
(i) Variation of displacement (x), velocity (v) and acceleration (a) with respect to time for different types of motion.  
	
		
			
			
 
			
			
			
Displacement(x) 
			
			
			
Velocity(v) 
			
			
			
Acceleration (a) 
			
		
		
			
			
(a) At rest
			
			
			
 
			
			
			
 
			
			
			
			
 
			
			
		
		
			
			
(b) Motion with  constant velocity
			
			
			
 
			
			
			

			 
			
			
			

			 
			
		
		
			
			
(c) Motion with constant acceleration
			
			
			
 
			
			
			
 
			
			
			

			 
			
		
		
			
			
(d) Motion with constant deceleration
			
			
			
 
			
			
			

			 
			
			
			

			
			
		
	
	
	
Scalar Quantities:- Scalar quantities are those quantities which require only magnitude for their complete specification.(e.g-mass, length, volume, density)
	
	
	
Vector Quantities:- Vector quantities are those quantities which require magnitude as well as direction for their complete specification. (e.g-displacement, velocity, acceleration, force)
	
	
	
Null Vector (Zero Vectors):- It is a vector having zero magnitude and an arbitrary direction.
	
When a null vector is added or subtracted from a given vector the resultant vector is same as the given vector.
Dot product of a null vector with any arbitrary is always zero. Cross product of a null vector with any other vector is also a null vector.
	
Collinear vector:- Vectors having a common line of action are called collinear vector. There are two types.
Parallel vector (θ=0°):- Two vectors acting along same direction are called parallel vectors.
Anti parallel vector (θ=180°):-Two vectors which are directed in opposite directions are called anti-parallel vectors.
	
	
Co-planar vectors- Vectors situated in one plane, irrespective of their directions, are known as co-planar vectors.
	
	
	
Vector addition:-
	
Vector addition is commutative-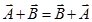  
Vector addition is associative-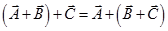   
Vector addition is distributive-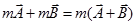   
	
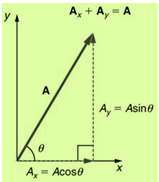
Triangles Law of Vector addition:- If two vectors are represented by two sides of a triangle, taken in the same order, then their resultant in represented by the third side of the triangle taken in opposite order.
       
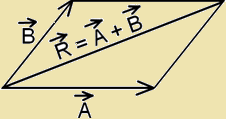
       Magnitude of resultant vector :-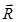
       R=√(A2+B2+2ABcosθ)
        Here θ is the angle between 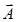 and .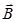
        If β is the angle between 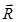 and ,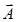
 then,
          
 
	
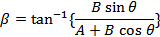
If three vectors acting simultaneously on a particle can be represented by the three sides of a triangle taken in the same order, then the particle will remain in equilibrium.
So,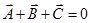  
	
Parallelogram law of vector addition:-
         
R=√(A2+B2+2ABcosθ),

 
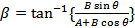
Cases 1:- When, θ=0°, then,
 R= A+B (maximum), β=0°
Cases 2:- When, θ=180°, then,
R= A-B (minimum), β=0°
Cases 3:- When, θ=90°, then,
R=√(A2+B2), β = tan-1 (B/A)
	
The process of subtracting one vector from another is equivalent to adding, vectorially, the negative of the vector to be subtracted. 
So,   
 
	
	
Resolution of vector in a plane:-
	
	
Product of two vectors:-
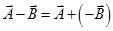
(a) Dot product or scalar product:-
 , 
 
Here A is the magnitude of 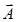, B is the magnitude of  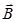and θ  is the angle between  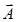and .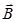
(i) Perpendicular vector:-
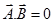
(ii) Collinear vector:-
When, Parallel vector (θ=0°),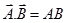
When, Anti parallel vector (θ=180°),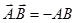
(b) Cross product or Vector product:-