Samyak Jain
Last Activity: 6 Years ago
|x| is always positive irrespective of sign of x.
|x + a| = x + a for x + a
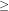
0 i.e. x
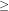
–a & |x + a| = –(x + a) for x + a
Given : x, |x+1|, |x–1| are first three terms of an AP.
 2|x+1| = x + |x–1|
2|x+1| = x + |x–1|.
Case 1. Let x
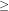
1. Then x+1 > 0 & x – 1
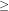
0 i.e. |x+1| = x+1 & |x – 1| = x – 1
So, 2|x+1| = x + |x–1|
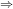
2(x+1) = x + x – 1
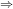
2 = – 1, which is false.
Case 2. Let –1
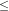
x
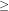
0 & x – 1
So, 2|x+1| = x + |x–1|
2(x+1) = x – (x – 1)
2x + 2 = x – x + 1 or 2x = – 1
i.e.
x = – 1/2. Clearly x = – 1/2 satisfies –1
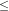
x
|x+1| = x + 1 = – 1/2 + 1 = 1/2 and |x – 1| = – (x – 1) = – (–1/2 – 1) = 3/2

– 1/2, 1/2 , 3/2 are the first 3 terms. Common diference d is 1/2 – (–1/2) = 1 and first term a is –1/2.
Sum of first n terms of an AP is (n/2)[2a + (n – 1)d].

sum of first 20 terms of the AP is (20/2)[2.(–1/2) + (20 – 1).1] = 10[ –1 + 19] = 10(18)
= 180
Case 3. Let x
So, 2|x+1| = x + |x–1|
– 2(x+1) = x – (x – 1)
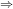
– 2x – 2 = x – x + 1 or – 2x = 3
i.e. x = – 3/2. Clearly x = – 3/2 satisfies x
|x+1| = – (x + 1) = – (–3/2 + 1) = 1/2 and |x – 1| = – (x – 1) = – (–3/2 – 1) = 5/2

– 3/2, 1/2 , 5/2 are the first 3 terms. Common diference d is 1/2 – (–3/2) = 2 and first term a is –3/2.

sum of first 20 terms of the AP is (20/2)[2.(–3/2) + (20 – 1).2] = 10[ –3 + 38] = 10(35)
= 350
Thus, the sum of first 20 terms of the AP is 180 or 350.





