Samyak Jain
Last Activity: 6 Years ago
Let r be the radius of given circle.
Distance between y-axis and centre C of the circle is r (

y-axis is tangent.)

C

(r,3).
Draw perpendicular from C on x-axis at say, M.
The perpendicular bisects the intercept made by the circle on the x-axis
because it is a chord of the circle.
Let the circle intersects x-axis at P and Q.

by Pythagoras theorem, CP
2 = CM
2 + PM
2i.e. r
2 = 3
2 + 1
2 = 10
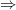
r =
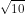
units

Centre of the circle is (
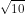
, 3).
Clearly, (
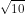
, 3) satisfies the equation
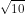
x – 3y – 1 = 0,
i.e., given line passes through the centre and is a diameter of the circle.

intercept made by the circle on the line
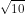
x – 3y – 1 = 0 is equal to
2r = 2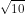 units
units 










