Sir please solve question number 2...................................
Sanjay Singh , 5 Years ago
Grade 12th pass
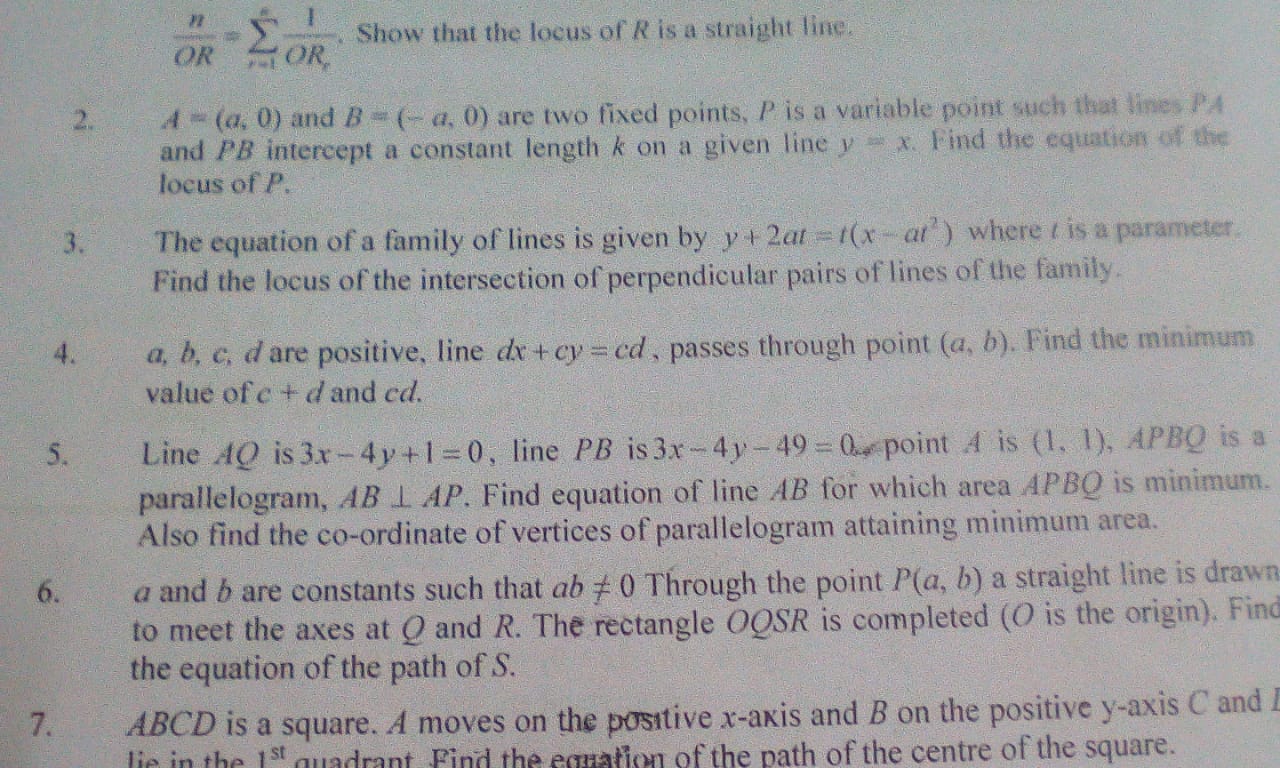
Analytical Geometry> Sir please solve question number 2..........
1 AnswersAditya Gupta
Last Activity: 5 Years ago
let P be (u, v).
now, write eqn of AP and BP. find the point of intersection of AP with line y= x (it will be an expression in a, u and v, for the time being lets call it (t, t)). similarly find the point of intersection of BP with line y= x (call it (z, z)).
then, k^2= (t – z)^2 + (t – z)^2
or k^2= 2(t – z)^2
since t and z are already known in terms of a, u and v, we finally have an eqn in a, u, k and v. now simply replace u and v by x and y respectively, and as a and k are constant, we would finally have the reqd locus. the ques would be a bit lengthy, but ans aa jaega
kindly approve :=)
Provide a better Answer & Earn Cool Goodies
Enter text here...
LIVE ONLINE CLASSES
Prepraring for the competition made easy just by live online class.
Full Live Access
Study Material
Live Doubts Solving
Daily Class Assignments
Ask a Doubt
Get your questions answered by the expert for free
Enter text here...
Other Related Questions on analytical geometry
The locus of the point represented by x= t^2 +t+1 and y=t^-t+1 is
analytical geometry
0 Answer Available
Last Activity: 2 Years ago
show that the centroids of the triangles of which three perpendiculars lie along the lines y=m1x,y=m2x,y=m3x lie on y(3+m2m3+m3m2+m1m2)=x(m1+m2+m3+3m1m2m3)
analytical geometry
0 Answer Available
Last Activity: 2 Years ago
show that the equation (ab-h²)(ax²+2hxy+by²+2gx+2fy)+af²+bg²-2fgh=0 represent a pair of straight lines and that these straight lines form a rhombus with the lines ax²+2hxy+by²=0
analytical geometry
0 Answer Available
Last Activity: 2 Years ago
A circle has its center on straight line 5x-2y+1=0 and cuts the x axis at two points whose absciasse are -5,3 find equation of the circle and it's radius.
analytical geometry
0 Answer Available
Last Activity: 2 Years ago
Prove that ax^2+by^2+cz^2 +2ux+2vy+2wz+d=0 represent a cone if u^2/a+v^/b+w^2/c=d
analytical geometry
0 Answer Available
Last Activity: 3 Years ago