0

Guest

Courses New

the sum of the slope of two tangents drawn from (-2,-1) to the hyperbola 2x^2 - 3y^2 = 6 a)4 b)9/2 c)7/2 d)7

the sum of the slope of two tangents drawn from (-2,-1) to the hyperbola  2x^2 - 3y^2 = 6
a)4
b)9/2
c)7/2
d)7

Grade:12

1 Answers

Samyak Jain
333 Points
4 years ago
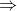
2 x2 – 3 y2 = 6  \Rightarrow  x2 / 3  –  y2 / 2 = 1    … given equation of hyperbola.
Comparing it with x2 / a2  –  y2 / b2  = 1, we get  a2 = 3  and  b2 = 2.
 
As we know that equation of tangent to hyperbola x2 / a2  –  y2 / b2  = 1 is 
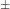
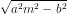
y = mx \pm \sqrt{a^2m^2 - b^2} , where m is the slope of the tangent.
 
So, the equation of tangent to given hyperbola is
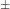
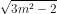
y = mx \pm \sqrt{3m^2 - 2}.
According to given condition, the tangent passes through (– 2, – 1), which will satisfy above equation.
\therefore – 1 = m(– 2) \pm \sqrt{3m^2 - 2}  \Rightarrow  – 1 + 2m = \pm \sqrt{3m^2 - 2}
Squaring both sides, we get (2m – 1)2 = 3m2 – 2
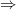
4m2 – 4m + 1 = 3m2 – 2  \Rightarrow  m2 – 4m + 3 = 0
Above quadratic equation in m has two roots, say m1 and m2 which are the slopes of tangents drawn from
 (– 2, – 1) to the given hyperbola.
Sum of roots = m1 + m2 = – (– 4) / 1 = 4 = required sum of slopes.

Think You Can Provide A Better Answer ?

Other Related Questions on Analytical Geometry

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More