Ask a Doubt
Get your questions answered by the expert for free
Enter text here...
Other Related Questions on Integral Calculus

The area of a square field is 640000cm2.what is its area in hectares
Integral Calculus
1 Answer Available
Last Activity: 2 Year ago(s)

Please solve this integration. I am facing difficulty in it How to solve this. Please solve anyone. Humble request
Integral Calculus
0 Answer Available
Last Activity: 2 Year ago(s)

Using laplace transform, solve d2y/dt2 + dy/dt = t2 +2t given that y=4 and y’=-2 and t=0
Integral Calculus
0 Answer Available
Last Activity: 2 Year ago(s)

how to solve this?this is interger type question .
Integral Calculus
0 Answer Available
Last Activity: 2 Year ago(s)

Integrate 0 to π/2 (x sin x cos x )/(a²cos²x + b²sin²x)²
Integral Calculus
1 Answer Available
Last Activity: 2 Year ago(s)




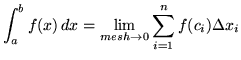 .
.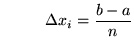
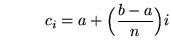
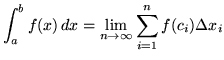 .
.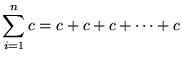 (n times)
(n times) 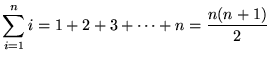
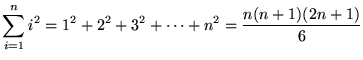
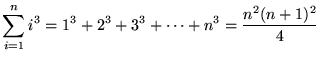
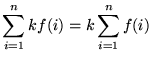 , where
, where