Solve this integral problem. ...................................
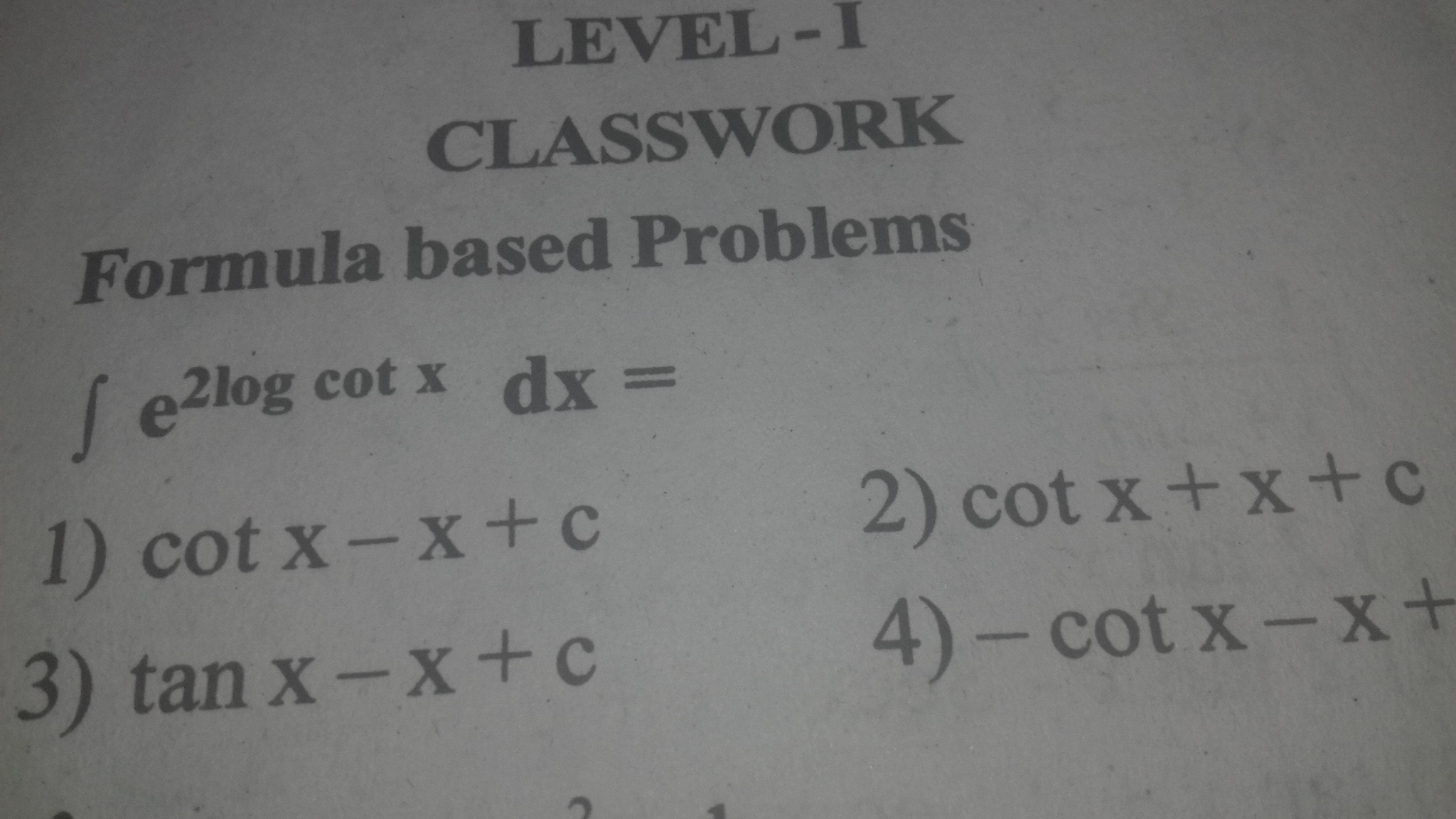
Get your questions answered by the expert for free

Last Activity: 2 Years ago

Last Activity: 2 Years ago

Last Activity: 2 Years ago

Last Activity: 3 Years ago

Last Activity: 3 Years ago