Block A of mass m and block B of mass M are connected by massless spring over a pulley on a rough plane with coefficient of friction `mu` . A force F is applied on block a to the left. When system is released find min valie of M to move block A towarda right

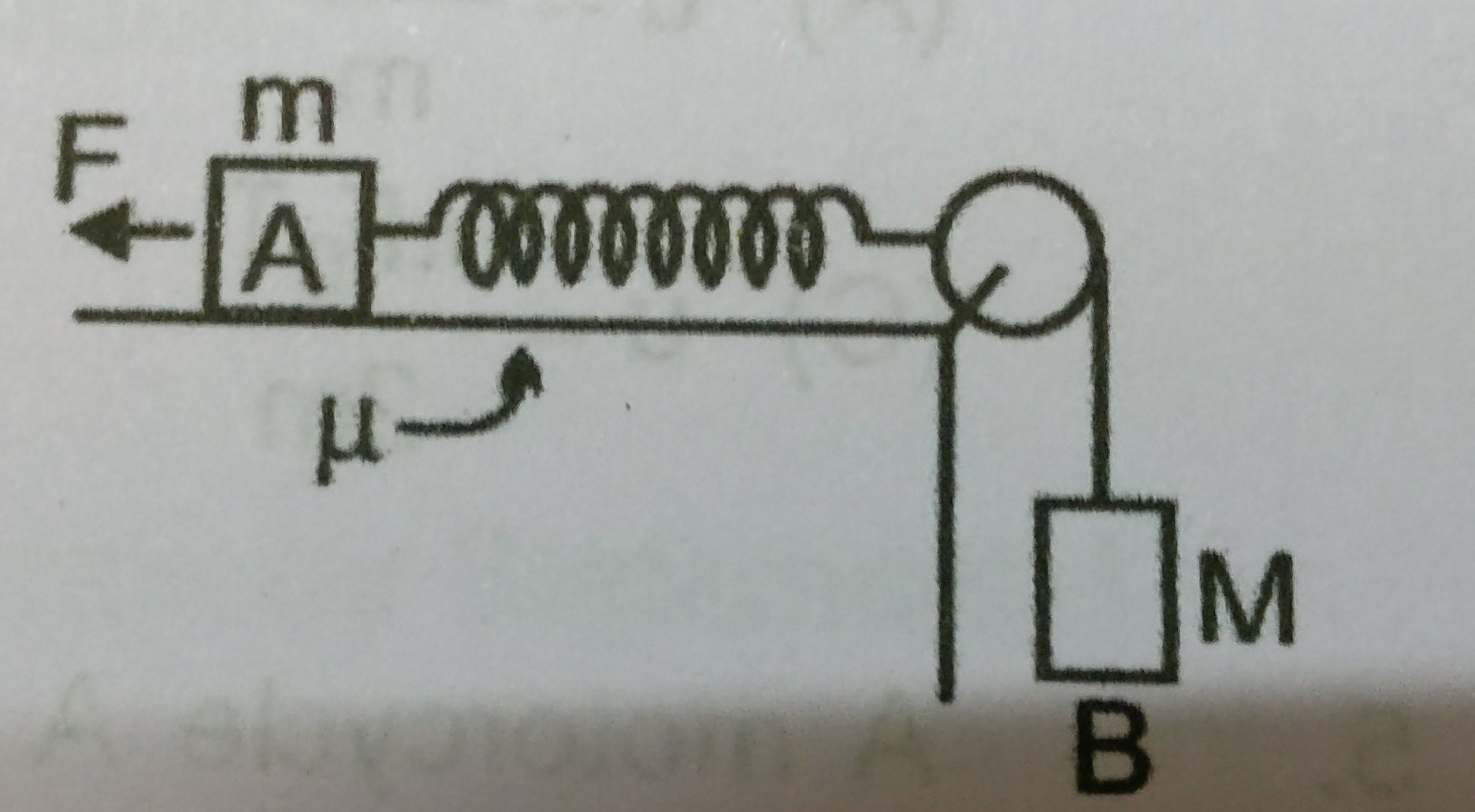
To determine the minimum value of mass M required to move block A to the right when a force F is applied to block A, we need to analyze the forces acting on both blocks and the effects of friction. Let's break this down step by step.

Understanding the Forces at Play

We have two blocks: Block A with mass m and Block B with mass M. Block A is on a rough plane, which means friction is a factor we need to consider. The coefficient of friction is given as μ. When a force F is applied to block A, it tries to move to the left, but we want to find the conditions under which it can move to the right instead.

Forces Acting on Block A

When the force F is applied to block A, the following forces act on it:

• The applied force F to the left.
• The frictional force opposing the motion, which is given by f_friction = μ * N, where N is the normal force on block A.
• The tension T in the spring connecting block A and block B, which will act to the right when block A is pulled to the left.

Forces Acting on Block B

For block B, the forces include:

• The weight of block B, which is M * g, acting downward.
• The normal force acting upward, which balances the weight.
• The tension T in the spring, which acts upward when block A is pulled to the left.

Setting Up the Equations

To find the minimum mass M that allows block A to move to the right, we need to set up the equations based on Newton's second law. For block A, the net force can be expressed as:

F - f_friction - T = m * a

For block B, the forces can be expressed as:

T = M * g - N

Frictional Force Calculation

The normal force N for block A on a rough plane is equal to its weight, which is m * g. Therefore, the frictional force becomes:

f_friction = μ * m * g

Combining the Equations

Substituting the expression for friction into the equation for block A gives:

F - μ * m * g - T = m * a

For block B, we can express T in terms of M:

T = M * g - m * g

Finding the Minimum Mass M

To find the minimum mass M that allows block A to move to the right, we need to set the acceleration a to zero (the point just before it starts moving). This leads us to:

F - μ * m * g - (M * g - m * g) = 0

Rearranging this gives:

F = μ * m * g + M * g - m * g

Solving for M, we have:

M = (F + m * g - μ * m * g) / g

Conclusion

The minimum value of mass M required to move block A to the right when a force F is applied to block A is given by the formula:

M = (F + m * g - μ * m * g) / g

This equation shows how the applied force, the mass of block A, and the frictional effects all play a role in determining the necessary mass of block B to initiate movement of block A to the right. By substituting the known values into this equation, you can find the specific minimum mass M needed for your scenario.