Hey there! We receieved your request
Stay Tuned as we are going to contact you within 1 Hour
One of our academic counsellors will contact you within 1 working day.
Click to Chat
1800-5470-145
+91 7353221155
Use Coupon: CART20 and get 20% off on all online Study Material
Complete Your Registration (Step 2 of 2 )
Sit and relax as our customer representative will contact you within 1 business day
OTP to be sent to Change
General equation of a plane is ax + by + cz + d = 0
Equation of the plane in Normal form is lx + my + nz = p where p is the length of the normal from the origin to the plane and (l, m, n) be the direction cosines of the normal.
The equation to the plane passing through P(x1, y1, z1) and having direction ratios
(a, b, c) for its normal is a(x – x1) + b(y – y1) + c (z – z1) = 0
The equation of the plane passing through three non-collinear points (x1, y1, z1),
(x2, y2, z2) and (x3, y3 , z3) is = 0
The equation of the plane whose intercepts are a, b, c on the x, y, z axes respectively is x/a + y/b + z/c = 1 (a b c ≠ 0)
Equation of YZ plane is x = 0, equation of plane parallel to YZ plane is x = d.
Equation of ZX plane is y = 0, equation of plane parallel to ZX plane is y = d.
Equation of XY plane is z = 0, equation of plane parallel to XY plane is z = d.
CXmhaU -8: Find the equation to the plane passing through the point (2, -1, 3) which is the foot of the perpendicular drawn from the origin to the plane.
hb: The direction ratios of the normal to the plane are 2, -1, 3.
The equation of required plane is 2(x –2) –1 (y + 1) + 3 (z –3) = 0
=> 2x – y + 3z –14 = 0
Angle between the Planes
Angle between the planes is defined as angle between normals of the planes drawn from any point to the planes.
Angle between the planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0 is
Note:
If a1a2 +b1b2 +c1c2 = 0, then the planes are perpendicular to each other.
If a1/a2 = b1/b2 = c1/c2 then the planes are parallel to each other.
CXmhaU -9: Find angle between the planes 2x – y + z = 11 and x + y + 2z = 3.
hb:
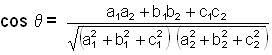
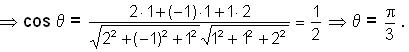
CXmhaU -10: Find the equation of the plane passing through (2, 3, –4), (1, –1, 3) and parallel to x-axis.
hb: The equation of the plane passing through (2, 3, –4) is
a(x – 2) + b(y – 3) + c(z + 4) = 0 ……(1)
since (1, –1, 3) lie on it, we have
a + 4b – 7c = 0 ……(2)
since required plane is parallel to x-axis i.e. perpendicular to YZ plane i.e.
1.a + 0.b + 0.c = 0 Þ a = 0 Þ 4b – 7c = 0 => b/7 = c/4
∴ Equation of required plane is 7y + 4z = 5.
Perpendicular Distance:
The length of the perpendicular from the point P(x1, y1, z1) to the plane ax + by + cz + d = 0 is|ax1 + by1 + cz1 + d / √a2 + b2 + c2|.
Family of Planes:
Equation of plane passing through the line of intersection of two planes u = 0 and v = 0 is u + λv = 0.
Intersection of a Line and Plane:
If equation of a plane is ax + by + cz + d = 0, then direction cosines of normal to this plane are a, b, c. So angle between normal to the plane and a straight line having direction cosines l, m ,n is given by cos θ = al + bm + cn / √a2 + b2 + c2.
Then angle between the plane and the straight line is π/2 – θ.
Get your questions answered by the expert for free
You will get reply from our expert in sometime.
We will notify you when Our expert answers your question. To View your Question
Win Gift vouchers upto Rs 500/-
Register Yourself for a FREE Demo Class by Top IITians & Medical Experts Today !