Equation of a Plane in Different Forms
Definition of Equation of a Plane in Different Forms
Consider the locus of a point P(x, y, z). If x, y, z are allowed to vary without any restriction for their different combinations, we have a set of points like P. The surface on which these points lie, is called the locus of P. It may be a plane or any curved surface. If Q be any other point on it’s locus and all points of the straight line PQ lie on it, it is a plane. In other words if the straight line PQ, however small and in whatever direction it may be, lies completely on the locus, it is a plane, otherwise any curved surface.
Equation of Plane in Different Forms
-
General equation of a plane is ax + by + cz + d = 0
-
Equation of the plane in Normal form is lx + my + nz = p where p is the length of the normal from the origin to the plane and (l, m, n) be the direction cosines of the normal.
-
The equation to the plane passing through P(x1, y1, z1) and having direction ratios
-
(a, b, c) for its normal is a(x – x1) + b(y – y1) + c (z – z1) = 0
-
The equation of the plane passing through three non-collinear points (x1, y1, z1),
-
(x2, y2, z2) and (x3, y3 , z3) is
 = 0
= 0 -
The equation of the plane whose intercepts are a, b, c on the x, y, z axes respectively is x/a + y/b + z/c = 1 (a b c ≠ 0)
-
Equation of YZ plane is x = 0, equation of plane parallel to YZ plane is x = d.
Equation of ZX plane is y = 0, equation of plane parallel to ZX plane is y = d.
Equation of XY plane is z = 0, equation of plane parallel to XY plane is z = d.
- Four points namely A (x1, y1, z1), B (x2, y2, z2), C (x3, y3, z3) and D (x4, y4, z4) will be coplanar if one point lies on the plane passing through other three points.
CXmhaU -8: Find the equation to the plane passing through the point (2, -1, 3) which is the foot of the perpendicular drawn from the origin to the plane.
hb: The direction ratios of the normal to the plane are 2, -1, 3.
The equation of required plane is 2(x –2) –1 (y + 1) + 3 (z –3) = 0
=> 2x – y + 3z –14 = 0
Angle between the Planes
Angle between the planes is defined as angle between normals of the planes drawn from any point to the planes.
Angle between the planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0 is 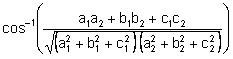
Note:
-
If a1a2 +b1b2 +c1c2 = 0, then the planes are perpendicular to each other.
-
If a1/a2 = b1/b2 = c1/c2 then the planes are parallel to each other.
CXmhaU -9: Find angle between the planes 2x – y + z = 11 and x + y + 2z = 3.
hb:
![]()
![]()
CXmhaU -10: Find the equation of the plane passing through (2, 3, –4), (1, –1, 3) and parallel to x-axis.
hb: The equation of the plane passing through (2, 3, –4) is
a(x – 2) + b(y – 3) + c(z + 4) = 0 ……(1)
since (1, –1, 3) lie on it, we have
a + 4b – 7c = 0 ……(2)
since required plane is parallel to x-axis i.e. perpendicular to YZ plane i.e.
1.a + 0.b + 0.c = 0 Þ a = 0 Þ 4b – 7c = 0 => b/7 = c/4
∴ Equation of required plane is 7y + 4z = 5.
Perpendicular Distance:
The length of the perpendicular from the point P(x1, y1, z1) to the plane ax + by + cz + d = 0 is|ax1 + by1 + cz1 + d / √a2 + b2 + c2|.
Family of Planes:
Equation of plane passing through the line of intersection of two planes u = 0 and v = 0 is
u + λv = 0.
Intersection of a Line and Plane:
If equation of a plane is ax + by + cz + d = 0, then direction cosines of normal to this plane are a, b, c. So angle between normal to the plane and a straight line having direction cosines l, m ,n is given by cos θ = al + bm + cn / √a2 + b2 + c2.
Then angle between the plane and the straight line is π/2 – θ.
- Plane and straight line will be parallel if al + bm + cn = 0
- Plane and straight line will be perpendicular if a/l = b/m = c/n.
CXmhaU -11: Find the equation of plane passing through the intersection of planes 2x – 4y + 3z + 5= 0, x + y + z = 6 and parallel to straight line having direction cosines (1, –1, –1).
hb: Equation of required plane be
(2x – 4y + 3z + 5) + λ(x + y – z – 6) = 0
i.e. (2 + λ)x + (–4 + λ)y + z(3 – λ) + (5 – 6λ) = 0
This plane is parallel to a straight line. So, al + bm + cn = 0
1(2 + λ) + (–1)(–4 + λ) + (–1)(3 – λ) = 0 i.e. λ = –3
∴ Equation of required plane is –x – 7y + 6z + 23 = 0
i.e. x + 7y – 6z – 23 = 0.
Bisector Planes of Angle between two Planes:
The equation of the planes bisecting the angles between two given planes a1x +b1y +c1z +d1 = 0 and a2x + b2y + c2z +d2 = 0 is

To read more, Buy study materials of 3D Geometry comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.
