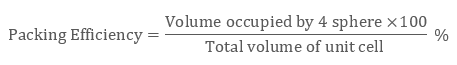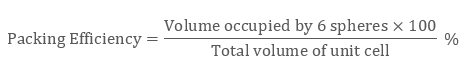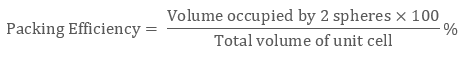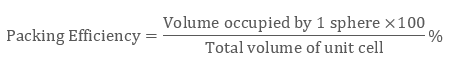Packing Efficiency
Table of contents |
Packing Efficiency
We know that constituent particles (atoms, molecules or ions) are arranged in different patterns in a unit cells. No matter how the particles are arranged in the lattice there is always some vacant space inside which we also call voids. The quantitative aspect of solid state can be done with the help of packing efficiency.
Image 1: Packing efficiency depends on arrangements of atoms and type of packing
Mathematically Packing Efficiency is:
Packing efficiency is defined as the percentage of space occupied by constituent particles packed inside the lattice. It can be calculated with the help of geometry in three structures namely:
-
HCP and CCP structures
-
Body-Centred Cubic Structures
-
Simple Cubic Lattice Structures
Factors Affecting Packing Efficiency
Following factors define packing efficiency of unit cell:
-
Volume of Unit Cell
-
Number of Atoms in a structure
-
Volume of atoms
HCP and CCP Structures
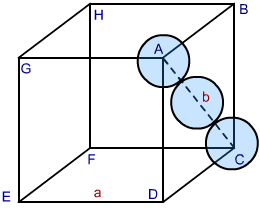
In both types of packing hexagonal closed packing or cubic closed packing the packing efficiency is same. In order to calculate packing efficiency in cubic closed structure, we consider a unit cell with edge length “a” and face diagonal AC to be “b”.
Image 2: CCP Structure
Looking at the ABCD face of the cube, we see a triangle ABC. Let the radius of the each sphere ball be ‘r’. Correlating radius and edge of the cube, we proceed as follows:
In △ ABC, by Pythagoras theorem we can write:
AC2 = BC2 + AB2
Since AC = b and BC = AB = a, substituting the values in the above relation we get
b2 = a2 + a2
b2 = 2a2
b = √2 a….. (1)
also edge b in terms of radius ‘r’ equals
b = 4r … (2)
From (1) and (2) we can write
4r = √2 a
or
a = 2 √2 r
As there are 4 spheres in a ccp structure unit cell, the total volume occupied by them will be
4 × 4 / 3 π r3
Also, total volume of a cube is (edge length)3 that is, ( a3) or in terms of r it is (2 √2 r)3, therefore packing efficiency will be:
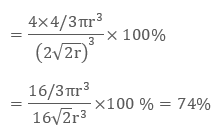
Therefore packing efficiency in fcc and hcp structures is 74%
Similarly in HCP lattice the relation between radius ‘r’ and edge length of unit cell “a” is r = 2a and number of atoms is 6
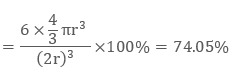
Examples: Be. Mg, Ti etc
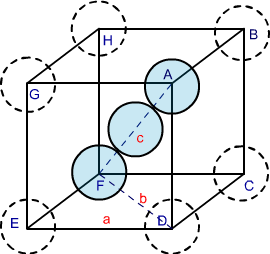
Body-Centred Cubic Structures
In body-centred cubic structures, the three atoms are diagonally arranged. To find the packing efficiency we consider a cube with edge length a, face diagonal length b and cube diagonal as c.
Image 3: BCC structure
In △ EFD according to Pythagoras theorem
b2 = a2 + a2
b2 = 2a2
b = √2 a
Now in △ AFD according to Pythagoras theorem
c2 = a2 + b2 = a2 + 2a2
c2 = 3a2
c = √3 a
If the radius of each sphere is ‘r’ then we can write
c = 4r
√3 a = 4r
r = √3/ 4 a
As there are two atoms in the bcc structure the volume of constituent spheres will be
2 × (4/3) π r3
Therefore packing efficiency of the body-centred unit cell is 68%.
Metals like iron and chromium fall under bcc category.
Simple Cubic Lattice
In simple cubic lattice, the atoms are located only on the corners of the cube. From the given figure we can see that the particles are in touch only at the edges.
Image 4: Simple cubic cell
So if radius of each atom is r and edge length of the cube is a, then we can correlate them as
2a = r
Since simple cubic unit cell contains only 1 atom, the volume of the unit cell with occupied 1 atom will be
4 / 3 π r3
And volume of unit cell will be ( a3) or ( 2a)3 that is, 8a3
Therefore the packing efficiency of simple unit cell is 52.4%
Examples falling under this category include metals like lithium and calcium.
Significance of Packing Efficiency
Packing efficiency holds importance in following ways:
-
It defines structure of solid
-
It specifies different properties of solids such as density, consistency and isotropy
-
Several attributes of solids can be derived with the help of packing efficiency
Watch this Video for more reference
More Readings