Representation of a Complex Number

 

A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary number satisfying i² =-1. In this expression, a is the real part and b is the imaginary part of the complex number. The complex number a + bi can be identified with the point (a, b) in the complex plane. A complex number whose real part is zero is said to be purely imaginary, whereas a complex number whose imaginary part is zero is a real number. Hence, the complex numbers contain the ordinary real numbers only.

In the early 19^th century, Karl Friedrich Gauss and William Hamilton independently and almost simultaneously proposed idea of redefining complex number as ordered pair of real numbers, i.e., a+ib = (a,b).

To each complex number there corresponds one and are point in plane, and conversely to each point in the plane there corresponds one and only are complex number. Because of this we often refer to the complex number z as the point z. A complex number may be represented in any of the following forms:

(a) Cartesian form (Geometric Representation):

Every complex number z = x+iy can be represented by a point on the Cartesian plane known as complex plane (Argand plane) by the ordered pair (x, y).

 

Length OP is called modulus of the complex number which is denoted by |z| and 0 is the argument or amplitude.

|z| = √(x² + y²) and tan θ = (y/x) (angle made by positive x-axis).

The concepts of argument, principal value and modulus are also related to the Cartesian form of the complex numbers. These terms have been discussed in detail at the end.

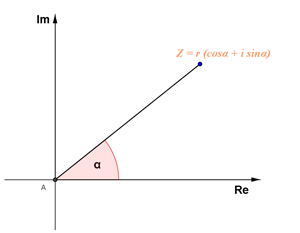
 (b) Trigonometric / Polar Representation:

In polar representation a complex number z is represented by two parameters r and ??. Parameter r is the modulus of complex number and parameter ?? is the angle with the positive direction of x-axis.

 z = r(cos ?? + i sin ??) where |z| = r, arg z = ?? I   = r(cos ?? - i sin ??).

Note: cos ?? + i sin ?? is also written as cis ??.

You can consult the Model Papers to get an idea about the types of questions asked.

 (c) Euler's Formula

Z =  re^iθ, |z|=r, arg z = θ

            =  re^-iθ

Proof of this formula is beyond scope of present discussion. A heuristic proof serving as motivation for this formula is by considering expansion.

e^x = 1+ x/1! + x²/2! + x³/3!

Put x = i θ

e^iθ = (1 - θ ²/2 + θ ⁴/4! ............) + (θ - θ ³/3! + θ ⁵/5! - .............)i

       = cos θ + sin θ

Note: If θ is real then cosθ = (e^iθ + e^-iθ)/2,

           sinθ = (e^iθ - e^-iθ)/2i

(d)  Vectorial Representation

Every complex number can be considered as the position vector of a point. If the point P represents the complex number z then   = z and | | = |z|.

The following video will provide you more clarity on the vector representation of a complex number:

 

Modulus, Argument and Principal Value Argument of a complex Number:

Modulus: The length of the vector OP is called the modulus or absolute value of the complex numbers z, and is denoted by |z|. It is a nonnegative real number given by the equation
|z| = √x²+y²
The only complex number with modulus zero is the number (0, 0).

Example: Consider the complex number z= -2+4i.   

Modulus |z| = √(-2)2 +42 = √20.

Argument: The angle between the positive real axis and the vector OP is called the argument of the complex numbers z, and is denoted by Arg(z).
More exactly Arg(z) is the angle through which the positive real axis must be rotated to cause it to have the same direction as vector OP. We assume that the point P is not the origin, P (0, 0).

If P = (0, 0), then |z| = 0 and Arg(z) is indeterminate.
Arg(z) is considered positive if the rotation is counterclockwise and negative if the rotation is clockwise.
|z| and Arg(z) are the polar coordinates of the point (x, y).
z = |z|{cos Arg(z) +i sin Arg(z)} is a polar representation of z.           

Note: Argument of a complex number is a many values function. If θ is the argument of a complex number then αnπ + θ; n ∈ I will also be the argument of that complex number. Any two arguments of a complex number differ by 2nπ. A complex number is completely defined only once its modulus and argument are defined.

0 is also a complex number as it can be written as 0= 0+0i. In this case, argument is not defined as this is the only complex number that is represented by its modulus.    

Examples: Arg (i) = π /2

Arg (-i) = -π /2

Arg (1) = 0

Arg (-1) = π

Arg (1+i) = π /4

Principal Value Argument: As the name suggests Principal Argument is one and only one value of Arg (z) which satisfies the inequality:

-π< Arg z ≤ π

Note that while argument is abbreviated by Arg (z), principal argument is written as arg(z).

The relation between Arg(z) and arg(z) is given by
Arg(z) = arg(z) +2nπ ,
where n ranges over all integers 0, ±1, ±2, … .

tan arg(z) = y/x = Im (z) / Re (z)

Example: If the principal polar representation of z is given by z= 4 (cos π/3 + i sin π/3), then find other instances of polar representation of z.

The other polar representations will occur at intervals of multiples of 2 π. Hence,
z = 4(cos 7π/3 + i sin7π/3). In fact the set z= 4 (cos π/3 + i sin π/3) represents all other polar representation of z.

Complex Numbers constitute an important part in the JEE exam. The topic usually fetches some direct questions and so it is important to master this topic to remain competitive in the JEE exam.
To read more, Buy study materials of Complex Numbers comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.