Bernoulli Trials and Binomial Distribution
Table of Content |
Bernoulli Trial
A random experiment which has only two mutually exclusive outcomes, namely ‘success’ and ‘not success’ or ‘failure’ is called Dichotomous Experiment.
If a dichotomous experiment is repeated n times and if in each trial the probability of success p (0 < p < 1) is constant, then all such trials are called Bernoulli trails.
This term is named after Jacob Bernoulli, a 17th century Swiss Mathematician.
Since, Bernoulli trial has only 2 possible outcomes, it can be framed as ‘yes’ or ’no’ question.
Example
-
Is the top card of the shuffled deck an ace?
-
Was the new born child a girl?
Binomial Distribution
An experiment of n repeated independent Bernoulli trails is called a Binomial Experiment.
Consider a Binomial experiment. Let the outcomes in each trial be a success (S) or Failure (F) with probability p and (1-p) = q respectively.
Let a random variable X = No. of successes
0 ≤ X ≤ n.
We want to find the probability of an event that the n trial result in exactly x successes and (n-x) failures is

Let A = {S S S…. S x times}
B= {F F F……F (n-x) times }
Since trials are independent,
P( A∩B) = P(a) . P(b)
= P(S).P(S)…..x times. P(F). P(F)…. (n-x) times
= p.p.p…..x times . q.q.q ….. (n-x) times
= px (q)n-x
Now, the number of possible orders of x successes and (n-x) failures in independent trials is nCx and these are mutually disjoint orders. Hence, probability that n trials result in exactly x successes and (n-x) failures in any order is given by
| P [X = x] = nCx px qn-x , 0 ≤ x ≤ n |
This is known as Binomial Distribution
A discrete random variable X is said to follow a Binomial distribution with parameters n and p if its probability mass function (pmf) if given by
P[X = x] = p(x) = nCx px qn-x , x = 0,1 , 2….n
0< p< 1, q = 1 – p,
n = 1, 2, 3….
Otherwise
P[X = x] for every x is xth term in the expansion of (q+p)n
Binomial distribution can be represented in tabular form as follows:
| X = x | 0 | 1 | 2 | ….. | x | ….. | n |
| P(x) | nC0 qn | nC1 pqn-1 | nC2 p2qn-2 | ….. | nCx pxqn-x | ….. | nCn pn |
From the above table we can see that,
-
P(x) ≥ 0 for all x
-
∑ p(x) = ∑ nCx px qn-x
= (q + p)n
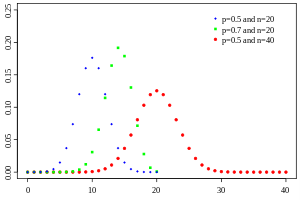
Fig: Probability Mass function of Binomial Distribution
Conditions for Binomial Distribution
The binomial distribution is used whenever each of the following is satisfied:
-
Trials of experiment are Bernoulli trials
-
The performance of a Bernoulli trial results in an outcome that can be classified either as a success or a failure
-
The number of trials (n) is finite
-
All n trials are independent
-
The probability of success is constant from trial to trial, i.e. the trials are repeated under identical conditions. Further, if P(success) = p and P(failure) = q, then p + q =1, 0 < p < 1
-
The random variable X denotes the number of successes x in n independent Bernoulli trials.
Notations:
-
X ~ B(n,p) denotes that X follows Binomial Distribution with parameters n and p.
Fig: Types of Probability Distribution
Mean and Variance of Binomial Distribution
The mean of random variable X denoted as E(X) is given by E(X) = np
The variance of random variable X denoted by Var (X) is given by Var(X) = npq
The standard derivation of random variable X is defined as the positive random variable X denoted by SD(X) is given by SD(X)= √Var(X) = √npq
Note: Mean > Variance that is, np > npq
Poisson Distribution
The Poisson binomial distribution, which describes the number of successes in a series of independent Yes/No experiments with different success probabilities.
A Poisson distribution is the probability distribution that results from a Poisson experiment.
Attributes of a Poisson Experiment
A Poisson experiment is a statistical experiment that has the following properties:
-
The experiment results in outcomes that can be classified as successes or failures.
-
The average number of successes (μ) that occurs in a specified region is known.
-
The probability that a success will occur is proportional to the size of the region.
-
The probability that a success will occur in an extremely small region is virtually zero.
Note that the specified region could take many forms. For instance, it could be a length, an area, a volume, a period of time, etc.
A Poisson Random Variable is the number of successes that result from a Poisson experiment. The probability distribution of a Poisson random variable is called a Poisson Distribution.
Given the mean number of successes (μ) that occur in a specified region, we can compute the Poisson probability based on the following formula:
Formula of Poisson
Suppose we conduct a Poisson experiment, in which the average number of successes within a given region is µ. Then, the Poisson probability is:
P(x; μ) = (e-μ) (μx) / x!
Where x is the actual number of successes that result from the experiment and is approximately equal to 2.71828
The Poisson distribution has the following properties:
-
The mean of the distribution is equal to μ.
-
The variance is also equal to μ.
Example
A fair coin is tossed 8 times. Find the probability that it shows heads
-
Exactly 5 times
-
A larger number of times than tails
-
At least once
Solution
Let X= Number of heads
P = Probability of getting head
P = 1/2
Q = 1- p = 1-1/2 = ½
Given: n = 8
X ~ B(8,1/2)
The p.m.f of X is given as
P(X = x) = p(x) = nCx px qn-x
that is, p(x) = 8Cx (1/2)x (1/2)8-x , x=0,1,2….8
- P (exactly 5 heads) = P[X = 5]
= P (5) = 8C5 (1/2)5 (1/2)8-5
= 8C3 (1/2)5 (1/2)3 [since nCx = nCn-x ]
= 7/32
Hence, the probability of getting exactly 5 heads is 0.21875
- P( getting heads larger number of times than tails )
= P[ X ≥ 5] = p(5) + p(6) + p(7) + p(8)
= 8C5 (1/2)5 (1/2)8-5 + 8C6 (1/2)6 (1/2)8-6 + 8C7 (1/2)7 (½)8-7 + 8C8 (1/2)8 (1/2)8-8
= 8C3 (1/2)5 (1/2)3 + 8C2 (1/2)6 (1/2)2 + 8C1 (1/2)7 (½) + 8C8 (1/2)8
= (½)8 [56 + 28 + 8 + 1] = 93/256
= P[X ≥ 5] = 0.36328
- P( getting heads at least once )
= P [ X ≥ 1] = 1-P[X = 0]
= 1- p(0)
= 1- 8C0 (1/2)0 (½) 8-0
= 1 – (1/2)8 = 1 - 1/256 = 255 / 256
P[ X ≥ 1] = 0.996
Hence, the probability of getting heads at least once is 0.996
Example
Suppose that 80% of all families own a television set. If 10 families are interviewed at random, find the probability that
-
Seven families own a television set
-
At most three families own a television set
Solution
Let X = Number of families who own a television
P = Probability of family who own a television set
P = 80% = 80/100 = 4/5
Q = 1- p = 1-4/5 = 1/5
Given: n =10
X ~ B(10,4/5)
The p.m.f of X is given as
P(X = x) = p(x) = nCx px qn-x
that is, p(x) = 10Cx 4/5x 1/510-x
- P (seven families own a television set) = P[X = 7] = p(7)
= 10C7 (4/5)7 (1/5)10-7
= 10C3 (4/5)7 (1/5)3 [since nCx = nCn-x ]
= 0.2013
Hence, the probability that seven families own a television set is 0.2013
- P (at most three families own a television set )
= P [X ≤ 3] = P[X = 0] + P[X = 1] + P[X = 2] + P[X = 3]
= p(0) + p(1) + p(2) + p(3)
= 10C0 (4/5)0 (1/5)10-0 + 10C1 (4/5)1 (1/5)10-1 + 10C2 (4/5)2 (1/5)10-2 + 10C3 (4/5)3 (1/5)10-3
= [1 + 40 + 45 * 16 + 120 * 64](1/5)10
= 8441/9765625
P [ X ≤ 3 ] = 0.00086
Hence, the probability that at most three families own a television set is 0.00086
Applications of Binomial Distribution
-
To find the probability of getting x heads in the experiment of tossing a fair coin n times. Here, X ~ B (n, p = ½)
-
To find the probability of getting success in the experiment of throwing a fair die or a pair of fair dice n times
-
To find the probability of correct answers in a multiple choice test consisting of n questions
-
To find the probability of success in any dichotomous experiment.
More Readings