The Method of Intervals (Wavy Curve Method)

 

Table of Content

The Method of Intervals Quadratic Expression Graphical Interpretations Summary of Important Points

The Method of Intervals

The Method of intervals (or wavy curve) is used for solving inequalities of the form f(x) =  > 0 ( < 0, < 0, or > 0) where n₁, n₂, ……, n_k, m₁, m₂, ……, m_p are natural numbers and the numbers a₁, a₂, ……, a_k; b₁, b₂,……, b_p are any real numbers such that a_i ¹ b_j, where i = 1, 2, 3, ……, k and j = 1, 2, 3, ……, p.

q  All zeros¹ of the function f(x) contained on the left hand side of the inequality should be marked on the number line with inked (black) circles.

q  All points of discontinuities² of the function f(x) contained on the left hand side of the inequality should be marked on the number line with un-inked (white) circles.

q  Check the value of f(x) for any real number greater than the right most marked number on the number line.

q  From right to left, beginning above the number line (in case of value of f(x) is positive in step (iii), otherwise, from below the number line), a wavy curve should be drawn to pass through all the marked points so that when it passes through a simple point³, the curve intersects the number line, and, when passing through a double point⁴, the curve remains located on one side of the number line.

q  The appropriate intervals are chosen in accordance with the sign of inequality (the function f(x) is positive whenever the curve is situated above the number line, it is negative if the curve is found below the number line). Their union represents the solution of inequality.

Remark:

(i)     Points of discontinuity will never be included in the answer.

(ii)    If you are asked to find the intervals where f(x) is non-negative or non-positive then make the intervals closed corresponding to the roots of the numerator and let it remain open corresponding to the roots of denominator.

¹The point for which f(x) vanishes (becomes zero) are called zeros of function e.g. x = a_i.

²The points x = b_j are the point of the discontinuity of the function f(x).

³If the exponents of a factor is odd then the point is called a simple point.

⁴If the exponent of a factor is even then the point is called a double point.

Illustration:

Let f(x) = . Find intervals, where f(x) is positive or negative.

Solution:

f(x) > 0  x Î (–5, –2)È(–1, 3)È(7, ¥)

and f(x) < 0  x Î (–¥, –5)È(–2, –1)È(3, 7).

Illustration:

Find the set of all x for which  x.

Solution:

We have  > 0 Þ < 0

Þ < 0

Þ < 0.                                       ……… (1)

There are five intervals x < –2, –2 < x < –1, –1 < x < –2/3, 
–2/3 < x < –1/2, x > –1/2.

The inequality (1) will hold for –2 < x < –1 and for –2/3 < x < –1/2.

Hence –2 < x < –1 an –2/3 < x < –1/2.

Quadratic Expression

The function f(x) = ax² + bx + c is called the quadratic expression. If a and b are the two distinct roots of the quadratic expression then it can be written as

ax² + bx + c = a (x – a) (x – b)

Now, considering every possibility of the roots of the equation.

Case I:

Roots are imaginary

Let one root of the quadratic equation be imaginary i.e. a = p + iq     then b = p – iq

and a(x – a)(x – b) = a [x –(p + iq)] [x – (p – iq)]

 = a [(x – p) – iq] [(x – p) + iq]

= a [(x – p)² + q²]

= a [(+)ve quantity]

so, sign of the expression depends on the sign of ‘a’, i.e. if a is   positive, then expression is positive. If a is negative, then expression     is negative.

Case II:

Roots are real and equal.

Let one root be a, then other root is also a.

Now, a(x – a)(x – b)    = a(x – a)²

 = a[(+)ve quantity]

again, the sign of the expression depends upon the sign of a.

Case III:

Roots are real and unequal

Let a and b be the two real roots and let a < b. Now consider following        cases.

(a)    x < a < b.

Þ (x – a) < 0

and   (x – b) < 0

so, a(x – a)(x – b) = a[(+)ve quantity]

Therefore, sign of the expression is same as sign of a

(b)    a < b < x.

Þ (x – a) > 0

and   (x – b) > 0

Therefore, sign of the expression is same as sign of a

(c)    a < x < b.

Þ (x – a) > 0

and   (x – b) < 0

so,    a(x – a)(x – b) = a[(–)ve quantity]

sign of the expression is to opposite to the sign of a.

The above result can be shown on real line as left hand side.
 

Graphical Interpretations

y = ax² + bx + c = a 

Þ                               …… (i)

This is an equation of a parabola with vertex at  and latus rectum .

Pause:

We shall discuss about parabola in detail in module VIII.

Now, in the rectangular co-ordinate system, if we shift origin to the    vertex , then equation (i) can be written as

Y = aX² or X² =  Y with x = X  y = Y 

To draw its graph, we observe the following :

Unless both roots and equal the curve should intersect x-axis twice.

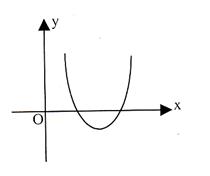
(i)     If a > 0 then Y has to be non-negative i.e., graph will be upward going infinitely i.e., of the shape as shown in figure.

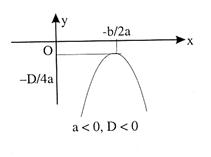
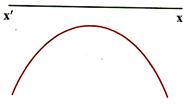
(ii)    If a < 0 then Y has to be non-positive i.e., graph will be downward going infinitely i.e., of the shape as shown in figure.

Now, the nature of roots of ax² + bx + c = 0 depends upon the fact that y = ax² + bc + c, the parabola with vertex  intersects x-axis one time, two times or not at all, which depends on the Y-coordinate of the vertex i.e.  on because parabola opens either upward of downward.

Case I:

When D < 0

Then vertex will be above or below x-axis corresponding to a > 0 or 
a < 0. Once vertex turns out to be above or below x-axis, then the whole graph is bound to be above or below x-axis respectively. Otherwise the graph will intersect x-axis i.e., ax² + bx + c = 0 will have real roots which contradicts the fact that D < 0.

Thus when D < 0 then ax² + bx + c > 0 x if a > 0 and ax² + bx + c < 0  x if a < 0

Case II:

When D = 0,

Then  = 0 i.e., the parabola just touches the x-axis and therefore, only one real root. In fact, that is the case when roots turn out to be real and equal.

In this case the equation of the parabola becomes

        y = a 

which confirms the statement made earlier.

i.e., a > 0 Þ y > 0  x

and a < 0 Þ y < 0  x

Thus, here too, the whole graph behaves as ‘a’.

Case III:

When D > 0

The vertex  will be above or below x-axis according to a < 0 or a > 0 respetively. When a < 0 then the vertex is above x-axis and so the graph has to extend downward infinitely so that it intersects x-axis at two distinct points i.e., the equation ax² + bx + x = 0 will have two real roots. Say, the roots are a and b and a < b.

And a < 0 then the vertex is below x-axis and so the graph has to extend upward infinitely to enable the existence of two distinct real roots.

When a < 0, then for all values of x lying between a and b, the corresponding y-coordinate on the graph is below x-axis i.e., the sign of 
(ax² + bx + c) will be same as that of ‘a’ for all x Î R and x Î (a, b) and the corresponding y coordinate on the graph is above x axis i.e., positive which confirms that (ax² + bx + c) behaves opposite to ‘a’ for all x Î (a, b). In same manner the corresponding graph can be seen true when a > 0.

Note:

(i)     In the above figures, we observe that Y-axis does not play any significant role in the above discussion.

(ii)    Under case (iii), we observe that if the roots are a & b then (a + b)/2 (i.e., mid-point of the line segment joining a & b = – b/2a i.e., a + b = – b/a.

(iii)    We know that multiplication by a constant (l) does not change the roots of the given quadratic equation i.e. ax² + bx + c = 0 and 
lax² + lbx + lc = 0 both have same set of roots.

Let us see the graphical significance of l.

(iv)   Having studied the graphs of the quadratic functions we may find the solution of the equation ax² + bx + c = 0 graphically.

Summary of Important Points

Depending on the sign of a and b² –4ac, f(x) may be positive negative or zero. This gives rise to the following cases:

(i)	a > 0 and b2 –4ac < 0 Û f(x) > 0  x Î R. In this case the parabola always remains above the x-axis.
(ii)	a > 0 and b2 –4ac = 0 Û f(x) > 0  x Î R. In this case the parabola always remains above the x-axis.
(iii)	a > 0 and b2 – 4ac > 0. Let f(x) = 0 have two real roots a and b (a<b) Then f(x) > 0  x Î (–¥, a)È(b, ¥) and f(x) < 0  x Î (a, b).
(iv)	a < 0 and b2 – 4ac < 0 Û f(x) < 0  x Î R In this case the parabola always remains below the x-axis.
(v)	a < 0 and b2 – 4ac = 0 Û f(x) < 0  x Î R. In this case the parabola touches the x-axis and lies below the x-axis.
(vi)	a < 0 and b2 – 4ac > 0 Let f(x)=0 have two real roots a and b (a<b). Then f(x) < 0 x Î(–¥, a)È(b, ¥) and f(x) > 0  x Î (a, b).

Illustration:

Let f(x) be a quadratic expression which is positive  x Î R. If g(x) = f(x) + f’(x) + f’’(x), then prove that g(x) > 0  x Î R.

Solution:

Let f(x) = ax² + bx + c. Then g(x) = f(x) + f’(x) + f’’(x)

= ax² + bx + c + (2ax + b) + 2a = ax² + (b + 2a) x + c + b + 2a.

Given f(x) = ax² + bx + c > 0  x Î R

Þ b² – 4ac < 0 and a > 0.                                    …… (1)

Now discriminant of equation g(x) = 0 is

D = (b + 2a)² –4a (c + b + 2a)

= b² + 4a² + 4ab – 4ac – 4ab – 8a²

= b² – 4a² – 4ac = (b² – 4ac) –4a² < 0 and a > 0 from (1)

Þ g(x) > 0  x Î R.

Illustration:

If f(x) = (a₁x + b₁)² + (a₂x + b₂)² +…+ (a_nx + b_n)², then prove that

(a₁b₁ + a₂b₂ + … + a_nb_n)² < .

Solution:

Given f(x) = (a₁x + b₁)² + (a₂x + b₂)² +……+ (a_nx + b_n)²            … (1)

or f(x) =  x² + 2(a₁b₁ + a₂b₂ +……+ a_nb_n)x +        .                                                             … (2)

From (1), f(x) > 0  x Î R

Þ from (2)

x² + 2(a₁b₁ + a₂b₂ +…+a_nb_n)x +  > 0,  x Î R.

Hence its discriminant D < 0         [ coefficient of x² is positive]

Þ 4(a₁b₁ + a₂b₂ +…+ a_nb_n)² < 4

Þ (a₁b₁ + a₂b₂ +…+ a_nb_n) < .

Illustration:

If ax² – bx + 5 = 0 does not have 2 distinct real roots, then find the minimum value of 5a + b.

Solution:

Let f(x) = ax² + bx + 5. Since f(x) = 0 does not have 2 distinct real roots, we have either f(x) < 0  x Î R.

But f(0) = 5 > 0, so f(x) > 0  x Î R. In particular f(–5) > 0

Þ 25a + 5b + 5 > 0 Þ 5a + b > – 1.

Hence the least value of 5a + b is –1.

To read more, Buy study materials of Quadratic Equation comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.