Relations
Table of Content |
|
|
What do we mean by Ordered Pairs in sets?
If we have two sets A and B, then (a, b) where a ∈ A & b ∈ B is called as the Ordered Pair. Moreover (a, b) ≠ ( b, a) in all the cases. This means, for the two sets A and B, depending upon the situation or requirement, we choose one of the sets as a primary set whose elements are treated as the first elements while the other will be secondary set whose elements are called as the second elements. Thus, if Set A is primary and Set B is secondary i.e. relation or mapping is from A to B, then corresponding ordered pairs will be of the form (a, b), such that a∈A & b∈B.
Ordered pairs are used in Cartesian product, relations and functions. We shall learn this with the examples in next section.
When two ordered pairs are equal?
Two ordered pairs (a1, b1) and (a2, b2) are said to be equal if
a1 = a2 & b1 = b2
Find the values of a and b if
(3a – 2, b + 3) = (2a – 1, 3)
b + 3 = 3, 3a – 2 = 2a – 1
a = 1, b = 0
Explain Cartesian Product of two sets
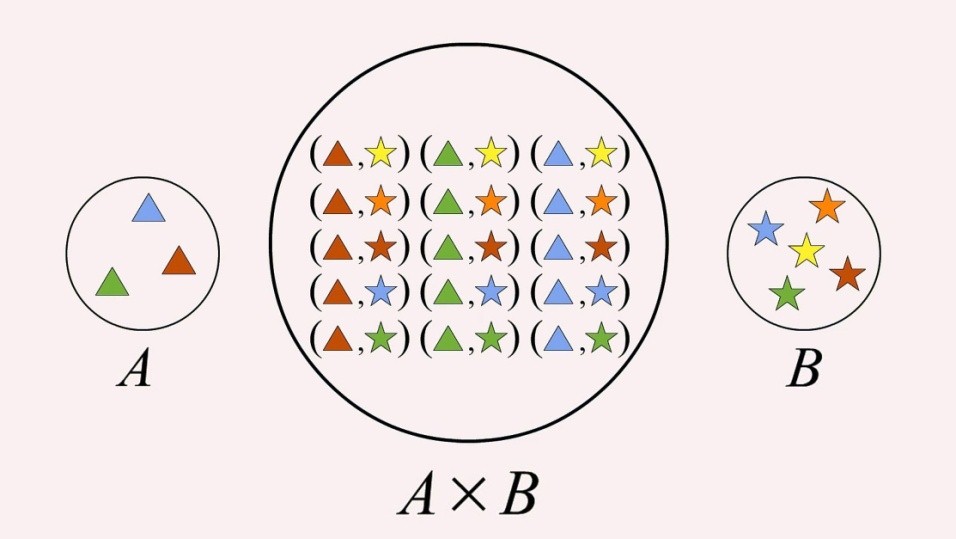
Cartesian product of the two sets is defined as the collection or set of all the possible ordered pairs between the two sets in proper order or sequence. Cartesian product of two sets A and B is denoted by A X B or B X A. Both A X B & B X A are different and accordingly the ordered pairs will be (a, b) or (b, a) respectively.
For Example, Let Set A = {1, 2, 3} and set B = {x, y}
Then Cartesian product of A and B i.e. A X B = {(1, x), (1, y), (2, x), (2, y), (3, x), (3, y)}
While B X A = {(x, 1), (x, 2), (x, 3), (y, 1), (y, 2), (y, 3)}
See the below image for another example on Cartesian product.
 |
 |
Define Relation in context to mathematics
Understanding relations requires basic knowledge of sets. A Set is a collection of well defined objects of particular kind. For Example a set of outcomes of dice, a sets of English alphabet.
Relation is always studied between two sets. If we have two non empty sets A and B then the relation R from set A to set B is represented by aRb, where a and b are the elements of the sets A and B respectively.
Relation from a set A to a set B is the subset of the Cartesian product of A and B i.e. subset of A x B. Relation can also be defined as an collection of ordered pairs (a, b) where a belongs to the elements from set A and b from set B and the relation is from A to B but not vice versa.
For Example
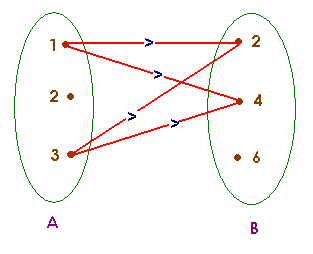
Consider a set A containing elements as {1, 2, 3} and set B contains elements as {2, 4, 6}. Then the relation between Set A and B from A to B will be set of any combinations from Set A to set B.
From the above diagram, we can see that Relation from A to B i.e. R will be set of {(1,2). (1, 4), (3, 2), (3, 4)}. This relation is a subset of the Cartesian product of two sets A X B.
Let’s take another example where, set A = {1, 2, 3} and set B = {1, 2, 3, 4, 5, 6, 7, 8, 9}.
If the Relation between A and B is as: elements of B is the squares of elements of set A, then the relation is written in the form of sets as:
R = {(a ,b): where b is square of a and a∈A & b∈B}
Then R = {(1, 1), (2, 4), (3, 9)}
Same as sets, relation may also be represented algebraically either by the Roster method or by the Set-builder method.
Relation can also be defined as a linear operation which establishes relationship between the element’s of two set’s according to some definite rule of relationship.
R: {(a,b) | (a,b) ∈ A x B and a R b}
Example
A is {2, 3, 5}
B is {1, 4, 9, 25, 30}
If a R b →b is square of a
Discreet element of relation are {(2,4), (3,9).(5, 25)}
A = {Jaipur, Lucknow, Bhopal}
B = {Rajasthan, Uttar pradesh, Madhya Pradesh}
aRb → a is capital of b,
A X B = {(Jaipur, Rajasthan), (Lucknow, Uttar Pradseh), (Bhopal, Madhya Pradesh}
Find the Total number of Relation from A to B
Let the number of relations from A to B be x.
Let A contain ‘m’ elements and B contains ‘n’ elements,
Number of element’s in A x B → m x n
Number of non void subset’s = C1mn+ C2mn+ …….. + Cmnmn = 2mn -1
Thus, for A = {1, 2, 3) & B = {x, y, z}
Number of non void subset’s or the number of possible relations =29- 1 = 511
What is Domain and Range of Relations?
For a relation R from a set A to set B, the set of all the first elements or coordinates or component’s of ordered pairs is called the Domain of R, whereas the set of all the second elements or coordinates or component’s of the ordered pairs in R is called as the range. Apart from Domain and Range, sometimes the knowledge of co-domain is also very important. Thus, the co-domain itself is the set B for a relation from set A to set B. That means, co-domain is all the possible outcomes for any relation R from set A to set B.
Let R: A → B (here R being the relation from set A to set B) then domain for this relation is defined as:
Domain: Set of all the first elements in R
{a | (a,b) ∈ R}
Range: Set of all the second elements in R
{b| (a,b) ∈ R}
Example
 A = {1, 4, 7 }; B = {1, 8, 16, 49}
A = {1, 4, 7 }; B = {1, 8, 16, 49}
Relation is aRb ⇒ a2 =b; a ∈ A, b ∈ B
Domain ={1, 4, 7}
Range = {1, 16, 49}
Co-Domain = {1, 8, 16, 49} It is the Set B itself.
Explain Inverse of a Relation
Inverse as the name suggest is the opposite or reciprocal of the Relation (R). It is denoted by R-1. This means if R is the relation from A to B then R-1 will be another relation from B to A.
Mathematically we may define it as:
R-1 = {(b,a) | (a,b) ∈R}
From the above mathematical definition, we may also conclude that domain of Relation aRb is converted to range of bRa (R-1). While range of aRb is now domain of R-1.
that is, Domain of R = Range of R-1
Example
A = {1, 2, 3, 4} & B = {1, 2, ……10}
xRy ⇒ y = 2x + 1 a ∈ A, y ∈ B
R = {(1, 3), (2, 5), (3, 7), (4, 9)}
Inverse Relation is
R-1→ {(3,1), (5, 2), (7, 3), (9, 4)}
What are the different types of Relations?
Relations in maths are of different types having different properties.
These types of relations are as:
-
Identity Relation
-
Reflexive Relation
-
Symmetric Relation
-
Transitive Relation
We shall learn this types of relations in detail later.
More Readings