Geometrical Meaning of Derivative at Point

 

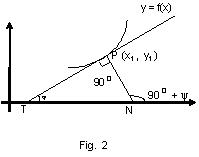
The derivative [f'(x) or dy/dx] of the function y = f(x) at the point P(x, y) (when exists) is equal to the slope (or gradient) of the tangent line to the curve y = f(x) at P(x, y).

Slope of tangent to the curve y = f(x) at the point (x, y) is m = tanθ = [dy/dx]_(x,y)

Equation of Tangent

The equation of tangent to the curve

 y = f(x) at the point P(x₁, y₁) is given by y – y¹ = [dy/dx]_(x,y) (x – x₁)

Notes:

(i) If dy/dx = 0 then the tangent to curve y = f(x) at the point (x, y) is parallel to the x-axis.

(ii) If dy/dx –> ∞, dx/dy = 0, then the tangent to the curve y = f(x) at the point (x, y) is parallel to the y-axis.

(iii) If dy/dx = tanθ > 0, then the tangent to the curve y = f(x) at the point (x, y) makes an acute angle with positive x-axis and vice versa.

Equation of Normal

The normal to the curve at the point P(x₁, y₁) is a line perpendicular to the tangent at the point P(x₁, y₁) and passing through it. The angle between a tangent and a normal at a point is always 90⁰. The equation of the normal to the curve y=f(x) at a given point P(x₁, y₁)is given by(x - x₁) + (y - y₁) [dy/dx]_(x1,y1)  = 0.
 

Equation of Tangent and Normal If Equation of the Curve is given in Parametric form

If the equation of the curve is in the parametric form x = f(t) and y = g(t), then the equations of the tangent and the normal are

            y – g(t) = g'(t)/f'(t)(x–f(t)) and f'(t)[x–f(t)] + g'(t) [y–g(t)] = 0 and  respectively

Illustration 9: If at each point of the curve y = x³ – ax² + x + 1 the tangents is inclined at an acute angle with the positive direction of the x-axis, then find the interval in which a lies.

Key concept: since the tangent is always inclined at an acute angle with the x-axis, hence and the use the concept of quadratic equation that ax² + bx + c > 0 for all x ÎR if a > 0 and D < 0

Solution:             y = x³ – ax² + x + 1 and the tangent is inclined at an acute angle with the positive direction of x-axis,

                              => dx/dy > 0             ∴ 3x² – 2ax + 1 >0, for all x ∈ R

                              => (2a)² – 4 (3)(1) < 0 => 4(a²  – 3)< 0 => (a – √3) (a + √3) < 0

                              ∴ – √3 < a < √3

Illustration 10:   The tangent to the curve y = x – x³ at a point P meets the curve again at Q. Prove that one point of trisection of PQ lies on y-axis. Find the locus of the other point of trisection.

Solution:             For y = x – x³, dy/dx = 1 – 3x²

                              Hence the equation of the tangent at the point P(x₁, y₁) is;

                               y – y₁= (1 – 3x₁²)(x – x₁)

                              It meets the curve again at Q (x₂, y₂)

                              Hence, (x₂– x₂³)– (x₁ – x₁³) = (1 – 3x₁²)(x₂ – x₁)

                              => (x₂ – x₁)[1- (x₂² + x₁x₂ + x₁²)] = (x₂ – x₁)(1 – 3x₁²)

                              => 1 – x₂²– x₁x₂– x₁² = 0   

                              or   

                              Since x₁ ¹ x₂, we have x₂ = - 2x₁

                              Q is (-2x₁, - 2x₁ + 8x₁³)

 If L₁(α, β) is the point of trisection of PQ then α = 2x₁ – 2x₁ / 3 = 0. Hence L₁lies on the y-axis. If L₂(h, k) is the other point of trisection, then h = x₁ 4x₁ /3 = –x₁ and k = y₁–4x₁ + 16x₁³/3

                              i.e. k = y₁ –4x₁ + 16x₁³/ 3 = –x₁ + 5x₁³

                              k = h - 5h³

                             ∴ locus of (h, k) is y = x – 5x³.
 

Angle of Intersections of two Curves

Let C₁: y= f(x) and C₂: y = g(x) be two curves. If two curves intersect at point P (x₁, y₁). Then the angle of intersection of two curves is defined as the angles between the tangents at their intersection. And is given by tan θ = f'(x₁) – g'(x) / 1 + f'(x₁)g'(x₁)

Note: 

(i) If the curves touch at P, then θ = 0 so that f ’ (x₁) = g ‘ (x₁)

(ii) If the angle θ = 90^o (π^c/2, right angle) i.e. Two tangents are perpendicular to each other then the curves are said to cut orthogonally, then f ‘(x₁). g ’(x₁) =- 1.

Illustration 11:   If the curves x²-4y²+c=0 and y² = 4x intersect orthogonally then find the range of c.

Solution: Curves will intersect if x² – 16 x + c = 0 has real roots. Thus c £ 64.

                              For x² – 4y² + c = 0, dy/dx = x/4y

                              For y² = 4x, dy/dx = 2/y

 If curves intersect orthogonally then x/4y.2/y = –1 => x = –2y² = –8x

                              => x = 0 => y = 0. But if y = 0, slope of both curves undefined.