Dual Nature of Matter and Photoelectric Effect

Dual Nature of Matter

In case of light some phenomenon like diffraction and interference can be explained on the basis of its wave character. However, the certain other phenomenon such as black body radiation and photoelectric effect can be explained only on the basis of its particle nature. Thus, light is said to have a dual character. Such studies on light were made by Einstein in 1905. Louis de Broglie, in 1924 extended the idea of photons to material particles such as electron and he proposed that matter also has a dual character-as wave and as particle.
 

Derivation of de-Broglie Equation

The wavelength of the wave associated with any material particle was calculated by analogy with photon.

In case of photon, if it is assumed to have wave character, its energy is given by

(According to the Planck’s quantum theory)

Where nth frequency of the wave and ‘h’ is is Planck’s constant

If the photon is supposed to have particle character, its energy is given by

E = mc²   ….… (ii)

(according to Einstein’s equation)

where ‘m’ is the mass of photon, ‘c’ is the velocity of light.

h c/λ   = mc²

The above equation is applicable to material particle if the mass and velocity of photon is replaced by the mass and velocity of material particle. Thus for any material particle like electron.

λ = h/mv   or λ =  where mv = p is the momentum of the particle.
 

Derivation of Angular Momentum from de Broglie Equation

If the wave is completely in phase, the circumference of the orbit must be equal to an integral multiple of wave length (λ) Therefore 2πr = nλ where ‘n’ is an integer and ‘r’ is the radius of the orbit But λ = h/mv ∴ 2πr = nh /mv   or mvr = n h/2π

“Thus, the number of waves an electron makes in a particular Bohr orbit in one complete revolution is equal to the principal quantum number of the orbit”.

The electron is revolving around the nucleus in a circular orbit. How many revolutions it can make in one second?

Let the velocity of electron be v m/sec. The distance it has to travel for one revolution 2πr, (i.e., the circumference of the circle).

Thus, the number of revolutions per second is = v / 2πr

Common unit of energy is electron volt which is amount of energy given when an electron is accelerated by a potential of exactly 1 volt. This energy equals the product of voltage and charge. Since in SI units 
coulombs x volts = joules, 1 eV numerically equals the electronic charge except that joule replaces coulombs.
 

Plank’s Quantum Theory 

When a black body is heated, it emits thermal radiations of different wavelengths or frequency. To explain these radiations, Max Planck put forward a theory known as Planck’s quantum theory. The main points of quantum theory are 

• Substances radiate or absorb energy discontinuously in the form of small packets or bundles of energy. 

• The smallest packet of energy is called quantum. In case of light the quantum is known as photon.  

• The energy of a quantum is directly proportional to the frequency of the radiation. E µ n (or) E = hn where n is the frequency of radiation and h is Planck’s constant having the value 6.626 X 10^–27 erg – sec or 6.626 X 10^–34 J–sec. 

• A body can radiate or absorb energy in whole number multiples of a quantum hn, 2hn,3hn………..nhn. Where ‘n' is the positive integer. 

• Neils Bohr used this theory to explain the structure of atom. 
  ​

Photoelectric Effect

Sir J.J. Thomson, observed that when a light of certain frequency strikes the surface of a metal, electrons are ejected from the metal. This phenomenon is known as photoelectric effect and the ejected electrons are called photoelectrons.

A few metals, which are having low ionization energy like Cesium, show this effect under the action of visible light but many more show it under the action of more energetic ultraviolet light.

An evacuated tube contains two electrodes connected to a source of variable voltage, with the metal plate whose surface is irradiated as the anode. Some of the photoelectrons that emerge from this surface have enough energy to reach the cathode despite its negative polarity, and they constitute the measured current. The slower photoelectrons are repelled before they get to the cathode. When the voltage is increased to a certain value V0, of the order of several volts, no more photoelectrons arrive, as indicated by the current dropping to zero. This extinction voltage (or also referred as stopping potential) corresponds to the maximum photoelectron kinetic energy i.e., eV_o = ½ mv²  

The experimental findings are summarized as below:

• Electrons come out as soon as the light (of sufficient energy) strikes the metal surface.

• The light of any frequency will not be able to cause ejection of electrons from a metal surface. There is a minimum frequency, called the threshold (or critical) frequency, which can just cause the ejection. This frequency varies with the nature of the metal. The higher the frequency of the light, the more energy the photoelectrons have. Blue light results in faster electrons than red light.

• Photoelectric current is increased with increase in intensity of light of same frequency, if emission is permitted i.e., a bright light yields more photoelectrons than a dim one of the same frequency, but the electron energies remain the same.

Light must have stream of energy particles or quanta of energy (hv). Suppose, the threshold frequency of light required to eject electrons from a metal is n0, when a photon of light of this frequency strikes a metal it imparts its entire energy (hv₀) to the electron.

“This energy enables the electron to break away from the atom by overcoming the attractive influence of the nucleus”. Thus each photon can eject one electron. If the frequency of light is less than v0 there is no ejection of electron. If the frequency of light is higher than v0 (let it be v), the photon of this light having higher energy (hv), will impart some energy to the electron that is needed to remove it from the atom. The excess energy would give a certain velocity (i.e, kinetic energy) to the electron.

hv = hv₀ + K.E

hv = hv₀ + ½ mv² 

Where, v = frequency of the incident light

hv₀ is the threshold energy (or) the work function denoted by Φ = hv₀ (minimum energy of the photon to liberate electron). It is constant for particular metal and is also equal to the ionization potential of gaseous atoms.

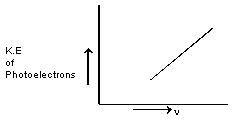
The kinetic energy of the photoelectrons increases linearly with the frequency of incident light. Thus, if the energy of the ejected electrons is plotted as a function of frequency, it result in a straight line whose slope is equal to Planck’s constant ‘h’ and whose intercept is hn₀­.