Solved Examples on Equilibrium

Question 1:

Calculate the pH of the solution when 0.1 M CH₃ COOH (50 ml) and 01. M NaOH (50 ml) are mixed, [Ka (CH₃COOH)=10^-5]

Solution:

CH₃ COOH $\rightleftharpoons$ CH₃ COO^_ + H⁺ …(I)

NaOH → Na⁺ + OH^-

H⁺ + OH^_ $\rightleftharpoons$ H₂O …(II)

(I) + (II)

CH₃COOH + OH^- CH₃COO^-+ H₂O . (III)

0.05-X 0.05-x x

Keq of eq. (III) = K_a/K_w

conc. of H₂O remain constant

10⁹ = x/(0.05-x)²

because value of eq. Const.is very high

here for x» 0.05

let 0.05-x=a

10⁹=0.05/a²

a = 7.07 $\times$ 10^-6

pOH= 6-log 7.07

pOH= 6 – 0.85

pH= 14-6+0.85 = 8.85

________________________________________________________________________________________

Question 2:

Calculate the pH at the equivalence point of the titration between 0.1M CH₃COOH ( 25 ml) with 0.05 M NaOH. Ka (CH₃COOH) = 1.8 $\times$ 10^–5.

Solution:

We have already seen that even though when CH₃COOH is titrated with NaOH the reaction does not go to completion but instead reaches equilibrium. We can assume that the reaction is complete and then salt gets hydrolysed because, this assumption will help us to do the problem easily and it does not effect our answer.

$[H^+]=\sqrt{\frac{K_wK_a}{C}}$

First of all we would calculate the concentration of the salt, CH₃COONa. For reaching equivalence point,

N₁V₁ = N₂V₂

0.1 ´ 25 = 0.05 ´ V₂

$\Rightarrow$ V₂ = 50 ml

Therefore [CH₃COONa] = (0.1 $\times$ 25)/75 =0.1/3

[H⁺] = $\sqrt{\frac{10^-^14\times 1.8\times 10^-^5}{0.1/3}}$

$\Rightarrow$ [H⁺] = 2.32 ´ 10^–5

$\Rightarrow$ pH = – log 2.32 ´ 10^–5 = 8.63

___________________________________________________________________________

Question 3:

Given the solubility product of Pb₃ (PO₄)₂ is 1.5 x 10^-32.Determine the solubility in gms/litre.

Solution:

Solubility product of Pb₃ (PO₄)₂ = 1.5 $\times$ 10^–32

Pb₃ (PO₄)₂ $\rightleftharpoons$ 3Pb²⁺ + 2PO₄^3-

If x is the solubility of Pb₃ (PO₄)₂

Then K_sp = (3x)³ (2x)²= 108 x⁵

x = 1.692 $\times$ 10^–7 moles/lit

Molecular mass of Pb₃(PO₄)₂ = 811

x = 1.692 ´ 10^–7 ´ 811 g/lit = 1.37 $\times$ 10^–4 g/lit

Solubility product is

K_sp(SrC₂O₄) = [Sr²⁺] [C₂O₄^2–] = (5.4 $\times$ 10^–4)^2- = 2.92 $\times$ 10^–7

________________________________________________________________________________________

Question 4:

What is pH of 1M CH₃COOH solution? To what volume must one litre of this solution be diluted so that the pH of resulting solution will be twice the original value. Given : K_a = 1.8 $\times$ 10^–5

Solution:

H₃CCOOH + H₂O $\rightleftharpoons$ H₃CCOO^– + H₃O⁺

t = 0 1M 0 0

-xM xM xM

__________________________________________

t = t_eq (1-x)M x x

pH = – log [H₃O⁺] = – log {4.2 $\times$ 10^–3} = 3 – log 4.2 = 2.37

Now, let 1L of 1M ACOH solution be diluted to VL to double the pH and the conc. of diluted solution be C.

H₃CCOOH + H₂O $\rightleftharpoons$ H₃CCOO^– + H₃O⁺

t = 0 C 0 0

– 1.8 $\times$ 10^–5 1.8 $\times$ 10^–5 1.8 $\times$ 10^–5

____________________________________________________

t= t_eq C – 1.8 $\times$ 10^–5 1.8 $\times$ 10^–5 1.8 $\times$ 10^–5

New pH = 2 $\times$ old pH = 2 $\times$ 2.37 = 4.74

pH = – log [H₃O⁺] = 4.74

[H₃O⁺] = 1.8 $\times$ 10^–5

C = 3.6 $\times$ 10^–5 L

on dilution

M₁V₁ = M₂V₂

1M $\times$ 1L = 3.6 $\times$ 10^–5 L $\times$ V₂

V₂ = 2.78 $\times$ 10⁴ L

________________________________________________________________________________

Question 5 :

Find the concentration of H⁺, HCO₃^- and CO₃^2-, in a0.01M solution of carbonic acid if the pH of this is 4.18.

Ka₁(H₂CO₃) = 4.45 $\times$ 10^–7 and Ka₂ = 4.69 $\times$ 10^–11

Solution:

pH = – log[H⁺]

4.18 = – log [H⁺]

[H⁺] = 6.61 $\times$ 10^–5

H₂CO₃ $\rightleftharpoons$ H⁺ + HCO₃^-

again, HCO₃^- $\rightleftharpoons$ H⁺ + CO₃^2-

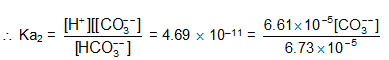
[CO₃^2-] = 4.8 $\times$ 10^–11

______________________________________________________________________________________

Question 6:

Calculate the molar solubility of Mg(OH)₂ in 1MNH₄Cl

K_spMg(OH)₂ = 1.8 $\times$ 10^–11

K_b(NH₃) = 1.8 $\times$ 10^–5

Solution:

Mg(OH)₂(s) $\leftrightharpoons$ Mg⁺⁺ + 2OH^– K₁ = K_sp

2NH₄⁺ + 2OH^- $\leftrightharpoons$ 2NH₄OH K₂ = 1/K²_b

____________________________________________________________________________________

Question 7:

An aqueous solution of metal bromide MBr₂ (0.05M) in saturated with H₂S. What is the minimum pH at which MS will ppt.?

K_sp =(MS) = 6 $\times$ 10^–21

Concentration of standard H₂S = 0.1

Ka₁(H₂S) = 1 $\times$ 10^–7

Ka₂(H₂S) = 1.3 $\times$ 10^–13

Solution:

In saturated solution of MS

MS(s) $\leftrightharpoons$ M⁺⁺ + S^2-

The precipitate of MS will form only if [S^––] exceeds the concentration of 1.2 $\times$ 10^–19

H₂S $\leftrightharpoons$ H⁺ + HS^– Ka₁

H₂S^– $\leftrightharpoons$ H⁺ + S^-- Ka₂

——————————————

H₂S $\leftrightharpoons$ 2H⁺ + S²^– K = 1.3 $\times$ 10^–20

[H⁺] = 0.109

pH = 0.96

___________________________________________________________________________________

Question 8 :

How much AgBr could dissolve in 1.0 L of 0.4 M NH₃? Assume that [Ag (NH₃)₂]⁺ is the only complex formed given, K_f [Ag(NH₃)₂⁺]=1.0 $\times$ 10⁸, Ksp (AgBr)= 5.0 $\times$ 10^-13

Solution:

AgBr $\rightleftharpoons$ Ag⁺ + Br^-

Ag⁺ + 2NH₃ $\rightleftharpoons$ Ag (NH₂)₂⁺

Let x= solubility ,

Then x= [Br^-]=[Ag⁺]+[Ag(NH₃)₂⁺]

x²=8.0´10^-6

$\Rightarrow$ x=2.8´10^-3 M

_______________________________________________________________________________________________

Question 9:

Equal volumes of 0.02 M Ag NO₃ and 0.02 M HCN were mixed. Calculate [Ag⁺] at equilibrium given, Ksp (AgCN)= 2.2 $\times$ 10^-16

Ka (HCN)= 6.2 $\times$ 10^-10

Solution.

Initially, assume complete precipitation

Ag⁺ + HCN → AgCN + H⁺, since the solution

were diluted to double volume

concentration of [H⁺] = 0.02/2 = 0.01M

Now consider the equilibrium

AgCN $\rightleftharpoons$ Ag⁺ + CN^- Ksp = 2.2´10^-16= [Ag⁺] [CN^-]

HCN $\rightleftharpoons$ H⁺ + CN^- Ksp = 6.2´10^-10= [H⁺] [CN^-]/[HCN]

Since every dissolved CN^- is also hydrolyzes into HCN up to certain extent.

__________________________________________________________________________________________________

Question 10 :

What is solubility of PbS (a) ignoring the hydrolysis of ions (b) including the hydrolysis of ions (assume pH of solution = 7).

Given that:

Solution:

a) Pbs(S) $\rightleftharpoons$ Pb⁺⁺ + S^––

K_sp = [Pb⁺⁺] [S^––] = S ´ S = S² = 7 ´ 10^–29

S = 8.4 $\times$ 10^–15

b) Including hydrolysis: The equilibria of interest are

Mass balance expression are:

[Pb²⁺]_o = [Pb²⁺] + [Pb(OH)]⁺ ------------- (a)

[S^--]_o = [S^––] + [HS^–] + [H₂S] ------- (b)

Substituting the value of [Pb(OH)⁺] from equation (i) into equation (a)

Substituting the values of [Pb⁺⁺] and [S^––] from equations (c) and (d), we get

On solving, Y = 1.0146 $\times$ 10^–10

______________________________________________________________________________________

Question 11:

Calculate the solubility of MnS in pure water. Assume hydrolysis of S^2– ions.

K_sp(MnS) = 2.5 $\times$ 10^–10

K_a1 and K_a2 of H₂S are 1 ´ 10^–7 and 1 $\times$ 10^–14 respectively

Solution:

Let molar solubility of MnS be XM

Mn(s) $\rightleftharpoons$ Mn²⁺ + S^2-

As K’_h >>K”_h, first step hydrolysis is almost complete,

x = [Mn²⁺] = [HS^–] = [OH^–]

Consider first step hydrolysis

At equilibrium, [Mn²⁺] [S^2–] = K_sp = 2.5 $\times$ 10^–10

Or n = (2.5 $\times$ 10^-10)/X²

x = 6.3 $\times$ 10^–4 M

_____________________________________________________________________________________________________________________

Question 12:

How much solid Na₂S₂O₃ should be added to 1.0 L of water so that 0.0005 mole Cd (OH₂) could just barely dissolve ?

K₁ and K₂ for S₂O₃^2- complexation with Cd²⁺ are 8.3 $\times$ 10³and 2.5 $\times$ 10², respectively. Ksp (Cd(OH)₂= 4.5 $\times$ 10^-15

Solution:

Cd(OH)₂ $\rightleftharpoons$ Cd²⁺ + 2OH^-

Ksp = [Cd²⁺] [OH^-]² =4.5´10^-15

Cd²⁺ + S₂O₃^2- $\rightleftharpoons$ Cd (S₂O₃)

Cd (S₂O₃) + S₂O₃^-- $\rightleftharpoons$ Cd (S₂O₃)₂^--

K₂=2.5 $\times$ 10²

Assume that S₂O₃^-- dose not hydrolyze

[Cd²⁺] + [Cd(S₂O₂)] + [Cd(S₂O₃)₂^2-] = 0.00050

[Cd²⁺]+K₁ [Cd ⁺⁺] S₂O₃^--] + K₁K₂ [Cd²⁺] [S₂O₃^2-]²= 0.00050

[Cd²⁺]= Ksp/[OH^-]²= 4.5 $\times$ 10^-9M

let [S₂O₃^2--]=x

then, 1+K₁x+K₁K₂x²= 1.1 $\times$ 10⁵

x = 0.2009

Wt/Mwt = 0.2009

wt = 0.2009 $\times$ 158 =31.74

_____________________________________________________________________________________________________

Question 13:

A solution contains a mixture of Ag⁺ (0.1M) and Hg₂²⁺ (0.1M) which are to be separated by selective precipitation. Calculate the maximum concentration of iodide ion at which one of them gets precipitated almost completely. What percentage of that metal ion is precipitated?

K_sp (AgI) = 8.5 $\times$ 10^–17

K_sp (Hg₂I₂) = 2.5 $\times$ 10^–26

Solution:

Let us first calculate [I^–] to precipitate AgI and Hg₂I₂

K_sp[AgI] = [Ag⁺] [I^–]

8.5 $\times$ 10^–17 = (0.1) [I^–]

[I^–] to precipitate as AgI = (8.5 $\times$ 10^-17)

K_sp(Hg₂²⁺) = [Hg₂I₂][I^–] = 8.5 $\times$ 10^–16 M

2.5 $\times$ 10^–26 = 0.1 [I^–]²

[I^–] to precipitate Hg₂I₂ = 5.0 $\times$ 10^–13 M

[I^–] to precipitate AgI is smaller. Therefore, Ag I will start precipitating first. On further addition of I^– more AgI will precipitate and when [I^–] ³ 5.0 ´ 10^–13 J, Mg₂I₂ will start precipitating. The maximum concentration of Ag⁺ at this stage will thus be calculated as:

K_sp(AgI) = [Ag⁺] [I^–]

8.5 $\times$ 10^–17 = [Ag⁺] (5.0 ´ 10^–13)

or, [Ag⁺] = 1.7 $\times$ 10^–4 M

Percentage of Ag⁺ remained precipitated = [(1.7 $\times$ 10^–4 M)/0/1] $\times$ 100 = 0.17%

Thus percentage of Ag⁺ precipitated = 99.83%

______________________________________________________________________________________________________

Question 14:

What [H⁺] must be maintained in a saturated H₂S (0.1M) to precipitate CdS but not ZnS, if [Cd⁺²] = [Zn⁺²] = 0.1 (M) initially?

Solution:

In order to prevent precipitating of ZnS,

[Zn⁺²] [S^–2] < K_sp (ZnS) = 1 $\times$ 10^–21

Ionic product

or, 0.1 [S^–2] < 1 $\times$ 10^–21

or, [S^–2] < 1 $\times$ 10^–20

This is the maximum value of [S^–2] before ZnS will precipitate

Let is the maximum value of [S^–2] be x.

Thus for H₂S $\rightleftharpoons$ 2H⁺ + S^–2

or, x = [H⁺] = 0.1 (M)

No ZnS will precipitate at and concentration of H⁺ greater than 0.1M.

_______________________________________________________________________________________________

Question 15:

Assuming the complete dissociation of HCl and the lead salt, calculate how much HCl is added to 0.001M lead salt solution to just percent precipitation when saturated with H₂S. The concentration of H₂S in its saturated solution is 0.1M

Ka (H₂S) = 1.1 $\times$ 10^–23

K_sp (PbS) = 3.4 $\times$ 10^–28

Solution:

We know, K_sp(PbS) = [Pb⁺²] [S^–2]

Since lead salt is completely dissociated, [Pb⁺²] is equal to the concentration of lead salt, i.e. [Pb⁺²] = 0.001M. If[S^–2] is the concentration of S^–2 required to just start precipitation of PbS.

[S^–2] = 3.4 $\times$ 10^–25

Now the addition of HCl with suppress the dissociation of H₂S to that extent that [S^–2] = 34 ´ 10^–25 (M)

HCl is completely ionised, \ [H⁺] = [HCl]

Let [HCl] be x’. Therefore [H⁺] = x’

H₂S $\rightleftharpoons$ 2H⁺ + S^–2

At equilibrium

[H₂S] = 0.1 – 3.4 $\times$ 10^–25 ≈ 0.1

[H⁺] = 2 $\times$ 3.4 $\times$ 10^–25 + x’ ≈ x’

[S^–2] = 3.4 $\times$ 10^–25

Related Resources:-

Click here for the Detailed Syllabus of IIT JEE Chemistry
Look into the Sample Papers of Previous Years
You can get the knowledge of Useful Books of Chemistry

To read more, Buy study materials of Chemical Equilibrium comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Ask a Doubt

Get your questions answered by the expert for free

Enter text here...

Book a Live class Live courses Ask question

Solved Examples on Equilibrium

Question 1:

Solution:

Question 2:

Solution:

Question 3:

Solution:

Question 4:

Solution:

Question 5 :

Solution:

Question 6:

Solution:

Question 7:

Solution:

Question 8 :

Solution:

Question 9:

Solution.

Question 10 :

Solution:

Question 11:

Solution:

Question 12:

Solution:

Question 13:

Solution:

Question 14:

Solution:

Question 15:

Solution:

Related Resources:-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Complete Self Study Package designed by Industry Leading Experts

Live 1-1 coding classes to unleash the Creator in your Child

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Ask a Doubt