Faraday’s Laws of Electrolysis

Table of Content

Faraday’s First Law
Faraday’s Second Law
Related Resources

The relationship between the quantity of electric charge passed through an electrolyte and the amount of the substance deposited at the electrodes was presented by Faraday in 1834, in the form of laws of electrolysis.

Faraday’s First Law

This law states that “the mass of a substance deposited or liberated at any electrode is directly proportional to the amount of charge passed” i.e., w a q (where w is the mass of the substance deposited or liberated and q is the amount of charge passed). This proportionality can be made into an equality by, w = zq

where z is the proportionality constant called the electrochemical equivalent. It is the mass of the substance in grams deposited or liberated by passing one coulomb of charge.

Faraday’s Second Law

This law states that “the mass of a substance deposited or liberated at any electrode on passing a certain amount of charge is directly proportional to its chemical equivalent weight”.

That is w a E where w is the mass of the substance in grams while E is its chemical equivalent weight in gms per equivalent =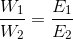 $\frac{W_1}{W_2}=\frac{E_1}{E_2}$ .

This law can be explained as follows.

Consider three reactions, such as:

Na⁺ + e^– → Na

Cu²⁺ + 2e^–-→ Cu

Al³⁺ + 3e^– → Al

Assume that these three reactions are occurring in three separate electrolytic cells connected in series.

When x moles of electrons are passed through the three cells, the mass of Na, Cu and Al deposited are 23x gms, 31.75x gms and 9x gms respectively.

We can see that 23, 31.75 and 9 gm/eq are the chemical equivalent weights of the three elements.

w = moles of electrons $\times$ E

The charge possessed by 1 mole of electrons

= 1.6 $\times$ 10^–19 $\times$ 6.023 x 10²³ ≈ 96500 C

This charge is called as 1 Faraday.

If we pass one Faraday of charge, it means that we are passing one mole of electron and by passing 1 Faraday of charge 1gm equivalent weight of the substance will be deposited or liberated.

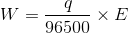
$W=\frac{q}{96500}\times E$

By combining the first and second law, we get

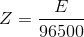
$Z=\frac{E}{96500}$

Note:

It should be made clear that the cathode is the electrode in which reduction reaction(s) occurs while the anode is the electrode where the oxidation reaction(s) occurs.

Do not relate the sign (positive or negative) of the electrode with the nature of the electrode.

Coulomb is the unit of electric charge. It is the amount of charge that moves past may given point in a circuit when a current of 1 ampere is supplied for one second.

For how long a current of three amperes has to be passed through a solution of AgNO₃ to coat a metal surface of 80cm² area with 0.005mm
thick layer? Density of silver is 10.5g/cc and atomic weight of
Ag is 108 gm/mol.

Solution:

Assuming that the coating has to be done on only one side of the surface, volume of Ag required for coating = (800x 0.005)/10 = 0.04cc

Mass of silver = 10.5 $\times$ 0.04 = 0.42gm

Moles of silver = 0.42/108 = 0.00389

Moles of electrons = 0.00389 (since Ag⁺ + e^– → Ag)

Charge passed = 0.00389 $\times$ 96500 = 375.385 coulombs

Time =375.385/3 = 125.1212 sec.

A solution of a salt of a metal of atomic weight ‘x’ was electrolysed for 150 minutes with 0.15A of current. The weight of the metal deposited was 0.783g. Find x. The specific heat of the metal = 0.057 cal/g°C.

According to the Dulong – Petit’s Law, approximate atomic weight of a metal ´ specific heat = 6.4

Solution:

We can use this law to calculate the approximate atomic weight of the metal first. This is equal to 6.4/0.057= 112.28 g/mol.

But this is not the value of x because x is the exact atomic weight.

From the data given it is possible to calculate the exact
equivalent weight, as,

Mass of the metal deposited = 0.783 g

Charge passed = 0.15 $\times$ 150 $\times$ 60 = 1350 coulombs

Equivalents of charge =1350/96500= 0.014

Equivalent weight = 0.783/0.014 = 55.93

Now, if we divide the approximate atomic weight by the exact equivalent weight, we will get the approximate valency of the metal in the salt.

approx. valency = 112.28/55.93 = 2.007

Since valency has to be an integer, n = 2

Exact atomic weight = 55.93 $\times$ 2 = 111.86gm/mol.

Question 1: Which of the following equations represent Faraday’s 1^st law of electrolysis?

a. w= zq

b. 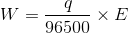$W=\frac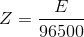{q}{96500}\times E$

c. $Z=\frac{E}{96500}$

d. 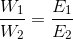$\frac{W_1}{W_2}=\frac{E_1}{E_2}$

Question 2: The charge possessed by 1 mole of electrons =

a. 1 F

b. 1 C

c. 96500 C

d. 96500 F

Question 3: 1 Faraday = .

a.92365 C

b.96500 C

c.92100 C

d.99500 C

Question 4: Which of the following equations is the combination of first and second law of electrolysis?

a. w= zq

b. 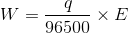$W=\frac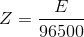{q}{96500}\times E$

c. $Z=\frac{E}{96500}$

d. $\frac{W_1}{W_2}=\frac{E_1}{E_2}$

Q.1	Q.2	Q.3	Q.4
a	c	b	c

Related Resources

Click here to get the Syllabus of IIT JEE Chemistry
Look into the Sample Papers for an idea about type of questions asked in IIT JEE.
You can look for Useful Books of Chemistry
You can also refer to Electrode Potential

To read more, Buy study materials of Electrochemistry comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.