Kohlrausch’s law

Table of Content

Kohlrausch’s Law States that
Uses of Kohlrausch’s law
Related Resources

Kohlrausch’s Law States that

"At infinite dilution, when dissociation is complete, each ion makes a definite contribution towards equivalent conductance of the electrolyte irrespective of the nature of the ion with which it Is associated and the value of equivalent conductance at infinite dilution for any electrolyte is the sum of contribution of its constituent ions", i.e., anions and cations. Thus,

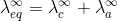
where,

$\lambda^\infty _e_q =Equivalence\ Conductivity\ at\ Infinite\ Dilution$

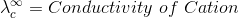
$\lambda^\infty _c =Conductivity\ of\ Cation$

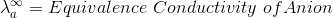
$\lambda^\infty _a =Equivalence\ Conductivity\ of Anion$

According to Kohlrausch’slaw. “conductivity of ions is constant at infinite dilution and it does not depend on nature of co-ions.”

For A_xB_y type electrolyte,

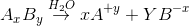
$A_xB_y \overset{H_2O}{\rightarrow} xA^+^y +YB^-^x$

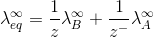
$\lambda ^\infty _e_q = \frac{1}{z}\lambda ^\infty _B +\frac{1}{z^-}\lambda ^\infty _A$

Here Z⁺and Z^- are the charges present on cation and anion.

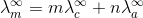
$\lambda ^\infty _m = m\lambda ^\infty _c +n\lambda ^\infty _a$

Here m and n are the number of moles of cations and anions.

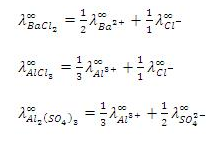
Uses of Kohlrausch’s law

Calculation of Molar Conductivity at Infinite Dilution For Weak Electrolytes

As already mentioned, the molar conductivity of weak electrolytes at infinite dilution cannot be determined experimentally, firstly because the conductance of such a solution is low and secondly because dissociation of such an electrolytes is not completed even at high dilutions.

The molar conductivity of such an electrolyte at infinite dilution can be calculated using Kohlrausch’s law

Calculation of Degree of Dissociation

According to Arrhenius theory of electrolytic dissociation, the increase in the molar conductivity with dilution is entirely due to the increase in the dissociation of the electrolyte; the molar conductivity at infinite dilution being maximum because the dissociation is almost complete.

Thus if $\lambda ^c_m$ is the molar conductivity of a solution at any concentration C and $\lambda _m^\infty$ the molar conductivity at infinite dilution (i.e. zero concentration), we will have

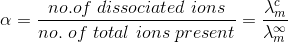
$\alpha = \frac{no. of\ dissociated\ ions}{no.\ of\ total\ ions\ present}=\frac{\lambda _m^c}{\lambda _m^\infty }$

However, this relationship is found to hold good only for weak electrolytes. The value of $\lambda _m^\infty$ for the weak electrolytes can be calculated , using Kohlrausch’s law, as discussed already in the first application.

Calculation of Dissociation Constant For a Weak Electrolyte

Knowing the degree of dissociation (as calculated above) the dissociation constant (K) of the weak electrolyte at concentration C of the solution can be calculated

using the formula

$K_c = \frac{C\alpha ^2}{1-\alpha }$

Calculation of Solubility of Sparingly Soluble Salt

Salts such as AgCl. BaSO₄, PbSO₄ etc which dissolve to a very small extent in water are called sparingly soluble salts.

A they dissolve very little, their solutions are considered as infinitely dilute. Further as their solutions are saturated, their concentration is equal to their solubility.

Thus by determining the specific conductivity (K) and the molar conductivity of such solutions , we have

$\lambda _m^o = \kappa \times \frac{1000}{Molarity} = \kappa \times \frac{1000}{Solubility}$

$\Rightarrow Solubility = \frac{\kappa \times 1000}{\lambda _m^o}$

Solved Example

Question:

From the given molar conductivities at infinite dilution, calculate $\lambda _m^\infty$ for NH₄OH.

$\lambda _m^\infty$ for Ba(OH)₂ = 457.6 ohm^-1 cm²mol^-1.

$\lambda _m^\infty$ for Ba(Cl)₂ = 240.6 ohm^-1 cm²mol^-1.

$\lambda _m^\infty$ for NH₄Cl = 129.8 ohm^-1 cm²mol^-1.

Solution:

$\lambda _m^\infty$ Ba(OH)₂ = $\lambda ^o_B_a_^2^+$ + $2\lambda ^o_O_H_^-$ ..(i)

$\lambda _m^\infty$ (BaCl₂ )= $\lambda ^o_B_a_^2^+$ + $2\lambda ^o_C_l_^-$ ...(ii)

$\lambda _m^\infty$ (NH₄Cl) = $\lambda ^o_N_H_4^+$ + $\lambda ^o_C_l_^-$ ..(iii)

$\because$ $\lambda _m^\infty$ f (NH₄OH) = $\lambda ^o_N_H_4^+$ + $\lambda ^o_O_H_^-$

= 1/2 eq. (i) + eq (iii) -1/2 eq (ii)

= $\frac{1}{2}\times 457.6+129.8-\frac{1}{2}\times 240.6$

= 238.3 ohm^-1 cm² mol^-1

Question 1:

According to Kohlrausch’s law, conductivity of ions is constant at

a. fixed temperature

b. infinite dilution

c. 1 M concentration

d. all the concentrations

Question 2:

According to Kohlrausch’s law, conductivity of ions at infinite dilutions does not depend on

a. nature of co-ions

b. temperature

c. pressure

d. concentration

Question 3:

Which of the following salts is not sparingly soluble one?

a. NaCl

b. AgCl.

c. BaSO₄

d. PbSO₄

Question 4:

What would be conductivity of MX₂ if conductivity of X- and M²⁺ is 5 ohm^-1cm²mol^-1 and 6 ohm^-1cm²mol^-1 respectively?

a. 10 ohm^-1cm²mol^-1

b. 11 ohm^-1cm²mol^-1

c.14 ohm^-1cm²mol^-1

d.17 ohm^-1cm²mol^-1

Q.1	Q.2	Q.3	Q.4
b	a	a	d

Related Resources

Refer to the Syllabus of IIT JEE
Look into the Past Year Papers of IIT JEE
You can also refer to Electrochemical Series

To read more, Buy study materials of Electrochemistry comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.