Matter and Its Nature
What is Matter?
Anything which has mass and occupies some space is called matter. Each and everything which we see around us is matter.
What about air? Neither we can see it nor has it mass!! Is it also matter?
The answer is yes! Air is a matter. We can’t see it but it occupies space. That is why only a limited amount of air can be filled in a balloon. Further, air has mass too. But the problem is that, its molecules move with such a high speed and the space between them is so large that we don’t feel the mass of air.
Remember when the molecules of gas collide with the wall of container they exert some force on it which is the cause of pressure of gas. Colliding molecule exerts force; this means it has some momentum. And if it has momentum, it must have mass too.
So, air is a matter.
Classification of Matter
Matter is classified at microscopic and macroscopic levels.
At microscopic level, it can be classified as solid, liquid and gas. These are the three physical states of matter.

These three states of matter and interconvertable by changing the conditions of temperature and pressure

At macroscopic level, matter can be classified as pure substances and mixtures. This classification of matter is based upon chemical composition of various substances. Pure substances can further be classified into elements and compounds

Elements: 
-
The primary stuff present in all the substance is known as element, whose smallest unit is known as atom.
-
Total 112 elements are known till date of which 92 are naturally occurring elements rest are results of artificial transmutation.
-
There are 88 metals, 18 non metals and 6 metalloids.
-
For example. Nitrogen, Hydrogen, Oxygen, Carbon etc.
 Compound:
Compound:
-
A non elemental pure substance is called a compound in which more than one atom of elements are linked by chemical bonds formed due to chemical reaction.
-
The resulting molecule is a electrically neutral particle of constant continuous composition.
-
For example: Water is a compound which is formed by combination of two elements hydrogen and oxygen.
Mixture:
-
 Mixtures are the aggregate of more than one type of pure substance whose chemical identity remains maintained even in mixtures. Their constituent ratio may vary unlike compound.
Mixtures are the aggregate of more than one type of pure substance whose chemical identity remains maintained even in mixtures. Their constituent ratio may vary unlike compound. -
For example sugar syrup is mixture of water and sugar. Gun-powder contains 75 % KNO3 , 10% sulphur and 15% carbon
-
There are two types of mixture (a) homogeneous (b) heterogeneous
-
Homogeneous mixtures are those whose composition for each part remains constant. For example aqueous and gaseous solution.
-
Heterogeneous mixtures are those whose composition may vary for each and every part. For example soil, concrete mixtures.
Physical and Chemical Properties of Matter
-
Physical Property: The property which can be measured without changing the chemical composition of the substance is known as physical property like mass, volume, density, refractive index etc.
-
Chemical Property: The property which can be evaluated at the cost of matter itself is known as chemical property. For example combustible nature of hydrogen gas can be verified by burning of hydrogen. The sweet taste of sugar by consuming it.
-
Physical Quantities : Many physical properties of substances are quantitative in nature. Such properties are called physical properties.
-
The measurement of any physical quantity consists of two parts:
-
The number and
-
The unit
-
-
Accuracy of the number is expressed using concepts of significant figures
-
The units of measurement are expressed in S.I. units
-
The units of any physical quantity are derived using the concept of dimensional analysis.
Example 1: |
|
Question: What is the difference between homogeneous and heterogeneous mixtures? Solution: A homogeneous mixture is a mixture which has uniform composition throughout the mixture. For example, mixtures of salt in water, sugar in water, copper sulphate in water, iodine in alcohol, alloy, and air have uniform compositions throughout the mixtures. A heterogeneous mixture is a mixture which has a non-uniform composition throughout the mixture. For example, Mixture of sodium chloride and iron fillings and mixture of salt and sulphur and also mixture of oil and water are all examples of heterogeneous mixtures |
Units for Measurement
All physical quantities have to be measured. The value of a physical quantity is expressed as the product of the numerical value and the unit in which it is expressed.
Fundamental Units:
Fundamental units are those units which can neither be derived from one another nor they can be further resolved into any other units.
The seven fundamental units of measurement in S.I. system.
|
Quantity |
Name of unit |
Abbreviation |
|
Mass |
Kilogram |
Kg |
|
Length |
Meter |
m |
|
Temperature |
Kelvin |
K |
|
Amount of substance |
Mole |
Mol |
|
Time |
Second |
S |
|
Electric current |
Ampere |
A |
|
Luminous intensity |
Candela |
Cd |
Derived unit:
Some quantities are expressed as a function of more than one fundamental units known as derived units. For example velocity, acceleration, work, energy etc.
|
Quantity with Symbol |
Unit (S.I.) |
Symbol |
|
Velocity (v) |
Metre per sec |
ms-1 |
|
Area (A) |
Square metre |
m2 |
|
Volume (V) |
Cubic metre |
m3 |
|
Density (r) |
Kilogram m-3 |
Kg m-3 |
|
Energy (E) |
Joule (J) |
Kg m2s-2 |
|
Force (F) |
Newton (N) |
Kg ms-2 |
|
Frequency (n) |
Hertz |
Cycle per sec |
|
Pressure (P) |
Pascal (Pa) |
Nm-2 |
|
Electrical charge |
Coulomb (C) |
A-s (ampere – second) |
Prefixes used in the SI System
|
Prefix |
Symbol |
Multiplier |
|
exa |
E |
1018 |
|
penta |
P |
1015 |
|
tera |
T |
1012 |
|
giga |
G |
109 |
|
mega |
M |
106 |
|
kilo |
k |
103 |
|
hecto |
h |
102 |
|
deka |
da |
101 |
|
deci |
d |
10-1 |
|
centi |
c |
10-2 |
|
milli |
m |
10-3 |
|
micro |
|
10-6 |
|
nano |
n |
10-9 |
|
pico |
p |
10-12 |
|
femto |
f |
10-15 |
|
atto |
a |
10-18 |
Units and Dimensional Analysis: Conversion of Units
The simplest way to carry out calculations that involve different units is to use dimensional analysis. In this method a quantity expressed in one unit is converted into an equivalent quantity with a different unit by using conversion factor which express the relationship between units:
Original quantity x conversion factor = equivalent quantity
(in former unit) (in other unit)
This is based on the fact that ratio of each fundamental quantity in one unit with their equivalent quantity in other unit is equal to one For example in case of mass
![]()
So 1 kg = 2.205 pond = 1000 gm

In this way any derived unit first expressed in dimension and each fundamental quantities like mass length time are converted in other system of desired unit to work out the conversion factor.
Example 2: |
|
Question: How unit of work / energy i.e. joule, in S.I. system is related with unit erg in C.G.S system Solution: Dimension of work = force x displacement = MLT-2´ L = ML2T-2 1 joule = 1 kg (1 metre)2´ (1see)-2
100 gm x (100)2 x1 em2 x (1 sec)-2 1000x10000 x 1 gm x1 cm2 x1 sec-1 1 joule = 107 erg |
Similarly we can deduce other conversion factor for other quantity in different unit by the dimensional analysis method
Another interesting example is the conversion of litre – atmosphere to joule (the SI unit of energy) by multiplying with two successive unit factors. Thus,
![]()
Knowing that![]() , we can write
, we can write
![]()
Hence 1 L atm = 101.325 J
Example 3: |
|
Question: What is the mass of 1 L of mercury in grams and in kilograms if the density of liquid mercury is Solution: We know the relationship, Also, We can write, mass = (volume) (density) Therefore, the mass of 1 L of mercury is equal to
The mass in kilograms can be calculated as (Remember, |

Question 1: Which of the following substances is an element?
a. Air
b. Water
c. Salt
d. Hydrogen
Question 2: Which of the following units is not used for measurement of mass?
a. Kg
b. g
c. mg
d. mL
Question 3: Coulomb is S.I. unit of
a. mass
b. electric charge
c. temperature
d. velocity
Question 4: Which of the following units is not the derived one?
a. Cd
b. Nm-2
c. m2
d. Kg m2s-2

|
Q.1 |
Q.2 |
Q.3 |
Q.4 |
|
d |
d |
b |
a |
Related Resources
-
You can also refer to past year papers of IIT JEE
-
Look here for the syllabus of chemistry for IIT JEE
-
Click here to refer laws of chemical combination
View courses by askIITians


Design classes One-on-One in your own way with Top IITians/Medical Professionals
Click Here Know More

Complete Self Study Package designed by Industry Leading Experts
Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child
Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!
Click Here Know MoreAsk a Doubt
Get your questions answered by the expert for free
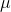
 ?
?