1800-150-456-789

Significant Figures and Scientific Notation

Precision and Accuracy

Precision refers to the closeness of various measurements for the same quantity while accuracy refers to the agreement of a particular value to the true value of the result.

For example, let the true value for a result be 2.00 g. A student ‘x’ takes two measurements and reports the result as 1.95 g and 1.93 g. These values are precise but not accurate. Another student ‘Y’ repeats the experiment and reports the result as 1.94 g and 2.05 g. These values are neither precise nor accurate.

A third student ‘z’ repeats the measurement and reports the result as 2.01g and 1.99 g. These values are both precise and accurate.

Precision refers to the closeness of various measurements for the same quantity. However, accuracy is the agreement of a particular value to the true value of the result.

Significant Figures

Significant figures are total number of digits in any number including the last digit whose value is uncertain.

Rules for Calculating Number of  the Significant Figures

  • All non-zero digits are significant. For example, 866 has three significant figures and 0.866 also has three significant figures..

  • Zeros to the left of the first non-zero digit in the number are not significant. For example, 0.008 has only one significant figure and 0.0085 has two significant figures.
    Zeros to the left of the first non-zero digit in the number are not significant

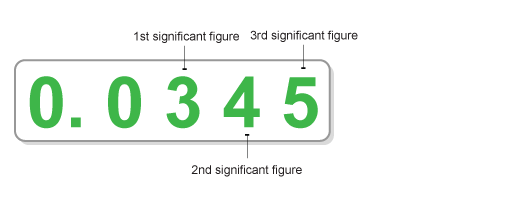
  • Zeros between non-zero digits are significant. For example, 3.05 has three significant figures.

  • Zeros to the right of the decimal point are significant. For example, 6.00, 0.60 and 0.6000 have 3, 2 and 4 significant figures.

  • If a number ends with zeros that does not have decimal, the zeros are not significant. For example: 3800 has two significant figures.

Rules for Determining Number of Significant Figures

Refer to the following video for scientific figures

Scientific Notation:

Scientific notation is the representation of numbers in N x 10n form.

Where N = a number with a single non-zero digit to the left of the decimal point.

n = some integer.

For example, 3800  can be expressed in scientific notation in the following forms depending upon whether it has two three or four significant figures:

Scientific Notation of 3800

3.8 x 103

Two Significant Figures

3.80 x 103

Three Significant Figures

3.8000 x 103

Four Significant Figures

0.38 x 104

Two Significant Figures

0.038 x 104

Two Significant Figures

  • Thus, we can write 531.598 as 5.31598 ×102 in scientific notation. Note that while writing it, the decimal had to be moved to the left by two places and same is the exponent (2) of 10 in the scientific notation.

  • Similarly, 0.00091 can be written as 9.1 × 10–4. Here the decimal has to be moved four places to the right and ( – 4) is the exponent in the scientific notation.

Calculation with Significant Figures:

Carrying out calculations with these numbers, the rule used is that the accuracy of the final result is limited to the least accurate measurement

Rounding Off

The rules employed for rounding off a number to the required number of significant digit are as follows

  • If the digit to be removed is more than 5, the digit to be retained is increased by one. for example, 2.486 If we have to remove 6, we have to round it to 2.49

  • If the digit to be removed is less than 5, the digit to be retained i.e. preceding number is not changed. For example, 5.334 if 4 is to be removed, then the result is rounded upto 5.33.

  • If the rightmost digit to be removed is 5, then the preceding number is not changed if it is an even number but it is increased by one if it is an odd number. For example, if 7.35 is to be rounded by removing 5, we have to increase 3 to 4 giving 7.4 as the result. However, if 7.25 is to be rounded off it is rounded off to 7.2.

Addition and Subtraction:

In addition and subtraction the final result should be reported to the same number of decimal places as the number with the minimum number of decimal places.

37.768 is rounded off in such a way that there is only one digit after the decimal.

For removing 6, 1 is added to 7 as 6 is greater than 5.

Example:  

2.435 + 1.23 = 3.665 

But the result would be reported only upto 2 decimal places so the answer would be 2.66.

Example :

44.341- 1.4432 = 42.8978.

But the result would be reported only upto 3 decimal places so the answer would be 42.898.

Multiplication and Division:

In multiplication and division, the final result should be reported as having the same number of significant digits as the number with least number of significant digits.

Multiplication and Division,

Example:

3.9898 x 0.23 = 0.917654

But the result would be reported in the form with two significant figures so the answer would be 0.92.

Multiplication and division.

Question 1: How many significant figures are there in 1001?

a.  4

b.  2

c.  1

d. 3

Question 2: In the final answer of the expression

\frac{(29.2-20.2)(1.79\times 10^{5})}{1.37}

the number of significant figures would be 

a. 1

b. 2

c. 3

d. 4

Question 3: Final result of the expression

10.23 + 11.234 - 22.1 – 11.2345

should be reported to the same number of decimal places as 

a. 10.23

b. 11.234

c. 22.1

d. 11.2345

Question 4: Which of the following alternatives represents an incorrect scientific notation for the number 123.45 ?

a. 12345.00 x 10-2

b. 1.23 x 102

c. 0.0123 x 103

d. 12.34 x 10-1

Q.1

Q.2

Q.3

Q.4

a

c

c

d

Related Resources

Live coursesAsk question