Gravimetric Analysis

Table of Content

Mass- Mass Relationship
Volume-Volume Relationship
Mass – Volume Relationship
Related Resources

Gravimetric analysis is an analytical technique based on the measurement of mass of solid substances and/or volume of gaseous species.

The gravimetric analysis is broadly classified into three heads.

Mass – mass relationship
Volume - volume relationship
Mass- volume relationship

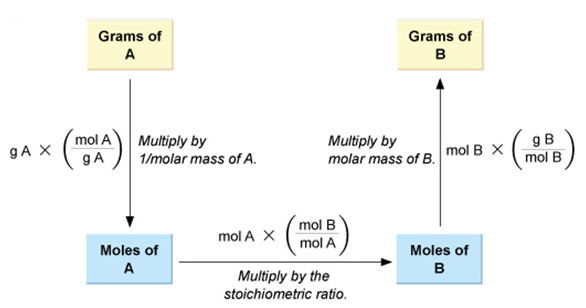
Mass- Mass Relationship

This relates the mass of a species (reactant or product) with the mass of another species (reactant or product) involved in a chemical reaction.

Let us consider a chemical reaction,

CaCO₃(s) CaO(s) + CO₂(g)

Let the mass of CaCO₃ taken be x g and we want to calculate the mass of CaO obtained by heating x g of CaCO₃. Then the moles of CaCO₃ taken would be (where M₁ represents the molar mass of CaCO₃).

According to the balanced reaction, the molar ratio of CaCO₃ and CaO is 1 : 1, so same number of moles ii.e. , of CaO would be formed.

Now for converting the moles of CaO into mass of CaO obtained, we need to multiply the moles of CaO with the molar mass of CaO. Let the molar mass of CaO be M₂, so the mass of CaO obtained by heating x g of CaCO₃ would be g.

CaCO₃(s) CaO(s) + CO₂(g)

We want to find out the volume of CO₂ evolved at STP by heating x g of CaCO₃. Then

Moles of CaCO₃ =

Moles of CO₂ evolved = (since molar ratio of CaCO₃ and CO₂ is 1 : 1)

Hence Volume of CO₂ evolved at STP = L

But, if the volume of CO₂ evolved is to be calculated at pressure P atm and temperature T K. Then,

Volume of CO₂ evolved at pressure P and temperature T = ( Using PV = nRT)

Volume-Volume Relationship

This relationship deals with the volume of a gaseous species (reactant or product) with the volume of another gaseous species (reactant or product) involved in a chemical reaction.

Let us consider the reaction, N₂(g) + 3H₂(g) → 2NH₃(g).

We are given x L of N₂ at pressure P atm and temperature TK and we want to know the volume of H₂ required to react with it at the same pressure and temperature.

Moles of N₂ =

Moles of H₂ required = (since molar ratio of N₂ & H₂ is 1 :3)

Hence Volume of H₂ required at same pressure & temperature = = 3 x L.

This result could also have been obtained by knowing that for a gaseous relation, at the same pressure and temperature, the moles of gas is directly proportional to volume of the gas (V a n since P & T are constant) or molar ratio and volume ratio are same.

Moles of H₂ required =
Hence Volume of H₂ required at pressure P’ atm & temperature T’K.

Refer to the following video for problems on stoichiometry

Now let us see the usefulness of these concepts in solving problems.

Solved Examples

Question 1

How much zinc should be added to 0.01 mol AgNO₃ solution to displace all the silver in the solution?

Solution:

The involved balanced reaction would be

Zn + 2AgNO₃ → Zn(NO₃)₂ + 2Ag

Moles of AgNO₃ in the solution = 0.01

Moles of Zn to be added to solution = 0.005

(since AgNO₃) and Zn are reacting the molar ratio of 2 : 1)

Hence Mass of Zn to be added to solution = 0.005 × 65.4 = 0.327 g

_______________________________________________________

Qestion 2

NaCI of 95% purity is used to prepare salt cake (Na₂SO₄) by the reaction,

2NaCI + H₂SO₄ → Na₂SO₄ + 2HCI

If the product (Na₂SO₄) is only % pure, what weight of NaCI is used up in producing 1 kg of the impure salt cake?

Solution:

Let the weight of NaCI used up in producing 1 kg of impure product be x g.

Mass of pure NaCI =

Moles of pure NaCI =

Moles of pure Na₂SO₄ =

Mass of pure Na₂SO₄ =

Hence x = 737.2 g

_________________________________________

Question 3:

KCIO₃ decomposes on heating in two possible ways as

KCIO₃ KCI + 3/2 O₂

2KCIO₃ KCI + 3KCIO₄

when 15 g of KCIO₃ were heated in an experiment, analysis of the product showed that 5.21 g of KCI and 4.59 g of KCIO₄ were formed. What was the weight of KCIO₃ remaining undecomposed? What fraction of KCIO₃ decomposed yielded KCIO₄?

Solution:

In order to calculate the weight of KCIO₃ remaining undecomposed, we need to find out eh total weight of KCIO₃ that decomposes. The weight of KCIO₃, that decomposes in second reaction would be known using the KCIO₄ data. Using KCIO₄ data, we would also calculate the weight of KCI obtained in second reaction. Since, total weight of KCI obtained is known to us, so the weight of KCI obtained in first reaction would also be known, using this we will find out the weight of KCIO₃ decomposed in first reaction.

Moles of KCIO₄ obtained =

Moles of KCI obtained in IInd reaction = (since molar ratio of KCIO₄ and KCI in IInd reaction is 3 : 1).

Moles of KCIO₃ that decomposes in IInd reaction = (since molar ratio of KCIO₄ and KCIO₃ in IInd reaction is 3 : 4)

Hence Mass of KCIO₃ that decomposes in IInd reaction = 122.5 = 5.41 g

Moles of KCI obtained in 1^st reaction = = 0.07 – 0.011 = 0.059

Moles of KCIO₃ that decomposes in 1^st reaction = 0.059

(since molar ratio of KCI and KCIO₃ in 1^st reaction is 1 : 1)

Mass of KCIO₃ that decomposes in 1^st reaction = 0.059 × 122.5 = 7.23 g

Total mass of KCIO₃ that decomposes in both the reaction = (5.41 +

7.23) = 12.64 g

Hence Mass of KCIO₃ that remain undecomposed = 15 – 12.64 = 2.36 g

Moles of O₂ evolved in 1^st reaction = 0.059 ×

Volume of O₂ evolved at STP in 1^st reaction = 0.059 × × 22.4 = 1.98 L

Fraction of KCIO₃ decomposed yielding KCIO₄ = = 0.36

Mass – Volume Relationship

This relationship deals with the volume of a gaseous species (reactant or product) with the mass of a solid species (reactant or product) involved in a chemical reaction.

Let’s take an example of combustion of Mg in air

2Mg + O₂ → MgO

In this reaction, one can find out the volume of O₂ required to react with given mass of Mg.

Let the mass of Mg taken is x g. So, the number of moles of Mg taken would be $\frac{x}{M}$ , where M is the molar weight of Mg.