Volumetric Analysis

 

Table of Content

Simple Titrations Acid- Base Titrations Redox Titrations Precipitation Titrations Complexometric Titrations ​Back Titration Double Titrations Related Resources

The volumetric analysis is an analytical method of estimating the concentration of a substance in a solution by adding exactly same number of equivalents of another substance present in a solution of known concentration.

The substance whose solution is employed to estimate the concentration of unknown solution is called titrant and the substance whose concentration is to be estimated is called titrate.

The volumetric analysis is divided into following types:

• Simple titration

• Back titration

• Double titrations

Simple Titrations

The aim of simple titration is to find the concentration of an unknown solution with the help of the known concentration of another solution.

Let us take a solution of a substance ‘A’ of unknown concentration. We are provided with solution of another substance ‘B’ whose concentration is known (N₁). We take a certain known volume (V₂ litre) of ‘A’ in a flask and start adding ‘B’ from burette to ‘A’ slowly till all the ‘A’ is consumed by ‘B’. This can be known with the aid of suitable indicator, which shows colour change after the complete consumption of ‘A’. Let the volume of B consumed is V₁ litre
According to the law of equivalents, the number of equivalents of ‘A’ would be equal to the number of equivalents of ‘B’.

Hence

N₁V₁ = N₂V₂,

where N₂ is the concentration of ‘A’.

Thus using this equation, the value of N₂ can be calculated.

There are four types of simple titration, namely

• Acid-base titrations

• Redox titrations

• Precipitation titrations and

• Complexometric titrations

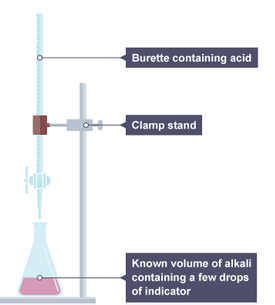Acid- Base Titrations

In this type of titration, the concentration of an acid in a solution is estimated by adding a solution of standard base and vice versa.

The equivalence point is detected by adding a few drops of a suitable indicator to the solution whose concentration is to be estimated.

An acid-base indicators gives different colours with acids and bases. The choice of indicator in a particular titration depends on the pH-range of the indicator and the pH change near the equivalence point.

For example,

Strong Acid - Strong Base Titration

In the titration of HCI vs NaOH, the equivalence point lies in the pH range of 4-10. Thus, methyl red (pH-range 4.2 to 6.3), methyl orange (pH-range 3.1 to 4.4) and phenolphthalein (pH-range 8.3 – 10) are suitable indicators of such titrations.

Weak Acid - Strong Base Titration

In the titration of CH₃COOH and NaOH, the equivalence point lies between 7.5 and 10. Thus, phenolphthalein is the suitable indicators.

Weak Base - Strong Acid Titration

In the titration of CH₃COOH and NH₄OH, the equivalence point lies between 4 to 6.5. Thus methyl orange and methyl red are suitable indicators.

Weak Acid - Weak Base Titration

In the titration of CH₃COOH and NH₄OH, the equivalence point lies between 6.5 and 7.5 and the pH change is not sharp at the equivalence point. Thus, no simple indicator can be employed to detect the equivalence point.

Redox Titrations

In a redox titration, an oxidant is estimated by adding reductant or vice-versa.

For example, Fe²⁺ ions can be estimated by titration against acidified KMnO₄ solution when Fe²⁺ ions are oxidized to Fe³⁺ ions and KMnO₄ is reduced to Mn²⁺ in the presence of acidic medium.

KMnO₄ functions as self-indicator as its purple colour is discharged at the equivalence point.

Mn + 8H⁺ + 5e^– → Mn²⁺ + 4H₂O

Fe²⁺    → Fe³⁺ + e^–] × 5

Mn + 8H⁺ + 5Fe²⁺ → Mn²⁺ + 5Fe³⁺ + 4H₂O

            (n=5)               (n=1)

In addition to acidified KMnO₄, acidified KCr₂O₇ can also be employed. Other redox titration are iodimetry, iodometry etc.

Iodimetry

This titration involves free iodine. Such direct estimation of iodine is called iodimetry.

This involves the titration of iodine solution with known sodium thiosulphate solution, whose normality is N. Let the volume of sodium thiosulphate used be V litre.

I₂ + 2Na₂S₂O₃ → 2NaI + Na₂S₄O₆

^{(n=2)        (n=1)}

Equivalents of I₂ = Equivalents of Na₂S₂O₃ used = N × V

Moles of I₂ = 

Mass of free I₂ in the solution = g

Iodometry

This is an indirect method of estimation of iodine. An oxidizing agent is made to react with excess of solid KI. The oxidizing agent oxidizes I^– to I₂.

This liberated I₂ is then made to react with Na₂S₂O₃ solution of normality N. Let the volume of thiosulphate solution required be V litre.

Oxidising Agent (A) + KI I₂  2NaI + Na₂S₄O₆

                                    +

                Reduced form of oxidizing agent

Equivalents of ‘A’ = Equivalents of I₂ = Equivalents of Na₂S₂O₃ used = N × V

Equivalents of I₂ liberated from KI = N × V

Equivalents of ‘A’ = N × V

Let the n-factor of ‘A’ in its reaction with KI be x, then

Mass of ‘A’ consumed =  × M_A (where M_A is the molar mass of A)

Precipitation Titrations

In a titration of this kind, cations and anions combine to form a compound of very low solubility. Thus, a solid residue separates out.

For example,

AgNO₃ + NaCI → AgCI¯ (white) + NaNO₃

BaCI₂ + H₂SO₄ → BaSO₄¯ (white) + 2HCI

Complexometric Titrations

In this type of titration, the titrate combines with the titrant to form complex salts. The complex salts may or may not be soluble. For example,

CuSO₄ + 4NH₄OH → [Cu(NH₃)₄]SO₄ + 4H₂O

AgNO₃ + 2KCN → K[Ag(CN)₂] + KNO₃

Refer to the following video for problem on acid-base titration

Back Titration

Let us assume that we have an impure solid substance ‘C’, weighing ‘w’ g and we are required to calculate the percentage purity of ‘C’ in the sample. We are also provided with two solutions ‘A’ and ‘B’, where the concentration of ‘B’ is known (N1) and that of ‘A’ is unknown.

For the back titration to work, following conditions are to be satisfied

• Compounds ‘A’, ‘B’ and ‘C’ should be such that ‘A’ and ‘B’ react with each other.

• ‘A’ and pure ‘C’ also react with each other but the impurity present in ‘C’ does not react with ‘A’.

• Also the product of ‘A’ and ‘C’ should not react with ‘B’.

Now we take out certain volume of ‘A’ in a flask (the equivalents of ‘A’ taken should be > equivalents of pure ‘C’ in the sample) and perform a simple titration using ‘B’. Let us assume that the volume of ‘B’ used be V₁ litre.

Equivalents of ‘B’ reacted with ‘A’ = N₁V₁

Hence Equivalents of ‘A’ initially = N₁V₁

In another flask, we again take some volume of ‘A’ but now ‘C’ is added to this flask. Pure part of ‘C’ reacts with ‘A’ and excess of ‘A’ is back titrated with ‘B’. Let the volume of ‘B’ consumed is V₂ litre.

Equivalent of ‘B’ reacted with excess of ‘A’ = N₁V₁

Hence Equivalents of ‘A’ initially = N₁V₁

Equivalents of pure ‘C’ = (N₁V₁ – N₁V₂)

Let the n-factor of ‘C’ in its reaction with ‘A’ be x, then the moles of pure ‘C’ = 

Hence Mass of pure ‘C’ =  × Molar mass of ‘C’.

Hence Percentage purity of ‘C’ =  ×  × 100
 

Double Titrations

The purpose of double titration is to determine the percentage composition of an alkali mixture or an acid mixture. In the present case, we will find the percentage composition of an alkali mixture. Let us consider a solid mixture of NaOH, Na₂CO₃ and some inert impurities, weighning ‘w’ g. We are required to find the % composition of this alkali mixture. We are also given an acid reagent (HCI) of known concentration M₁ that can react with the alkali sample.

We first dissolve this mixture in water to make an alkaline solution and then we add two indicators, (Indicators are substances that indicate colour change of solution when a reaction gets completed), namely phenolphthalein and methyl orange to the solution. Now, we titrate this alkaline solution with standard HCI.

NaOH is a strong base while Na₂CO₃ is a weak base. So it is obvious that NaOH reacts first with HCI completely and Na₂CO₃ reacts only after complete NaOH is neutralized.

NaOH + HCI → NaCI + H₂O                       …..(i)

Once NaOH has reacted completely, then Na₂CO₃ starts reacting with HCI in two steps, shown as

Na₂CO₃ + HCI → NaHCO₃ + NaCI           ……. (ii)

NaHCO₃ + HCI → NaCI + CO₂ + H₂O      …… (iii)

It is clear that when we add HCI to the alkaline solution, alkali is neutralized and the pH of the solution decreases. Initially the pH decrease would be rapid as strong base (NaOH) is neutralized completely.

When Na₂CO₃ is converted to NaHCO₃ completely, the solution is still weakly basic due to the presence of NaHCO₃ (which is weaker as compared to Na₂CO₃). At this point, phenolphthalein changes colour since it requires this weakly basic solution to show its colour change.

When HCI is further added, the pH again decreases and when all the NaHCO₃ reacts to form NaCI, CO₂ and H₂O the solution becomes weakly acidic due to the presence of the weak acid (H₂CO₃). At this point, methyl orange changes colour as it requires this weakly acidic solution to show its colour change.

Thus in general, phenolphthalein shows colour change when the solution contains weakly basic NaHCO₃ along with other neutral substances while methyl orange shows colour change when solution contains weakly acidic H₂CO₃ along with other neutral substances.

Let the volume of HCI used up for the first and the second reaction be V1 litre (this is the volume of HCI used from the beginning of the titration up to the point when phenolphthalein shows colour change) and the volume of HCI require for the third reaction be V₂ litre (this is the volume of HCI used from the point where phenolphthalein had changed colour upto the point when methyl orange shows colour change). Then,

Moles of HCI consumed by NaHCO₃ = Moles of NaHCO₃ reacted = M₁V₂

Moles of NaHCO₃ formed from Na₂CO₃ = M₁V₂

Moles of Na₂CO₃ in the mixture = M₁V₂

Mass of Na₂CO₃ in the mixture = M₁V₂ × 106

% of Na₂CO₃ in the mixture = 

Moles of HCI used in te reaction (i) and (ii) = M₁V₁

Moles of HCI used in reaction (ii) = M₁V₂

Moles of HCI used in reaction (i) = (M₁V₁ – M₁V₂)

Hence Moles of NaOH = (M₁V₁ – M₁V₂)

Mass of NaOH = (M₁V₁ – M₁V₂) × 40

% of NaOH in the mixture = 

Here, we have determined the percentage composition of the mixture using mole concept, as the balanced reactions were available. If we were to solve this by equivalent concept, then the procedure adopted would be

NaOH + HCI → NaCI + H₂O                       …….(i)

Na₂CO₃ + HCI → NaHCO₃ + NaCI             …….(ii)

^{(n=1)            (n=1)         (n=1)}

Phenolphthalein shows end point after reaction (ii)

NaHCO₃ + HCI → NaCI + CO₂ + H₂O      ……...(iii)

         ^{(n=1)            (n=1)}

and methyl orange shows end point after reaction (iii).

At phenolphthalein end point,

(Equivalents of HCI)₁ = Equivalents of NaOH + Equivalents of Na₂CO₃ (n=1)  = M₁V₁

or (Equivalents of HCI)₁ = Equivalents of NaOH +½ Equivalents of Na₂CO₃ (n=2) ..(iv)

At methyl orange end point,

(Equivalents of HCI)₂ = Equivalents of NaHCO₃ reacted (n=1) = Equivalents of NaHCO₃ produced (n=1) = Equivalents of Na₂CO₃ (n=1)

Hence M₁V₂ = Equivalents of Na₂CO₃ (n=1) = ½ Equivalent of Na₂CO₃ (n=2) ……..(v)

Subtracting equation (v) from equation (iv),

Equivalents of NaOH = (M₁V₁ – M₁V₂)

Hence Moles of NaOH = (M₁V₂ – M₁V₂)    (since n-factor of NaOH is 1)

Hence % of NaOH in the mixture = 

Equivalents of Na₂CO₃ (n=1) = M₁V₂

and moles of Na₂CO₃ = M₁V₂ (since n-factor of Na₂CO₃ is 1)

Hence % of Na₂CO₃ in the mixture = 

In the above case, we have taken alkali mixture of NaOH & Na₂CO₃. But other alkali mixtures can also be taken. 

(i) If a mixture of NaOH and NaHCO3 has been taken Equivalents of NaOH = Equivalents of HCI required upto phenolphthalein end point. Equivalents of NaHCO3 = Equivalents of HCI required from phenolphthalein end point to methyl orange end point. (ii) If a mixture of Na2CO3 and NaHCO3 has been taken ½ Equivalent of Na2CO3 (n=2) = Equivalents of HCI required upto phenolphthalein end point ½ Equivalents of Na2CO3 (n=2) + Equivalents of NaHCO3 initially (n=1) = Equivalents of HCI required from phenolphthalein end point to methyl orange end point. (iii) If a mixture of NaOH, Na2CO3 and NaHCO3 has been taken Equivalents of NaOH + ½ Equivalents of Na2CO3 (n=2)? = Equivalents of HCI required upto phenolphthalein end point ½ Equivalents of Na2CO3 (n=2) + Equivalents of NaHCO3 initially (n=1) = Equivalents of HCI required from phenolphthalein end point to methyl orange end point.

Solved Example

Question: A solution contains a mixture of Na2CO3 and NaOH. Using phenolphthalein as indicator, 25 ml of mixture required 21 ml of 1.1 N HCI for the end point. With methyl orange as indicator, 25 ml of solution required 25 ml of the same HCI for the end point. Calculate grams per litre of each substance in the mixture. Solution: Since, the volume of HCI required in titration using methyl orange is greater than the volume of HCI required using phenolphthalein, this means that the titration is carried out separately two times using phenolphthalein and methyl orange indicators, respectively. NaOH + HCI → NaCI + H2O                       …… (i) Na2CO3 + HCI → NaHCO3 + NaCI           ……. (ii) NaHCO3 + HCI → NaCI + CO2 + H2O      …….. (iii) Thus, the volume of HCI used in third reaction = (25 – 21) = 4.0 ml Hence Moles of HCI used in third reaction = 4.0 × 10–3 × 1.1 Moles of NaHCO3 reacted = 4.4 × 10–3 Moles of NaHCO3 produced = 4.4 × 10–3 Hence Moles of Na2CO3 present in 25 ml = 4.4 × 10–3 Hence Mass of Na2CO3 present in 1 litre = 4.4 × 10–3 × 106 × 40 = 18.656 g Moles of HCI reacted in second reaction = 4.4 × 10–3 Moles of HCI used in first two reactions = 21 × 10–3 × 1.1 = 23.1 × 10–3 Hence Moles of HCI used in first reaction = (23.1 – 4.4) × 10–3 = 18.7 × 10–3 Moles of NaOH present in 25 ml = 18.7 × 10–3 Hence Mass of NaOH present in 1 litre = 18.7 × 10–3 × 40 × 40 = 29.92 g

Question 1: Which of the following types of titration is not a simple titration?

a. Acid-base titrations

b. Back titration

c. Precipitation titrations 

d. Complexometric titrations

Question 2: According to the law of equivalents,

a.N₂V₁ = N₁V₂,

b.N₁V₂ = N₂V₁,

c.N₁V₁ = N

d. V = N₂V₂,

Question 3:  Which of the following conditions is nor required for the back titration to work ?

a. Compounds ‘A’, ‘B’ and ‘C’ should be such that ‘A’ and ‘B’ react with each other.

b. ‘A’ and pure ‘C’ also react with each other but the impurity present in ‘C’ does not react with ‘A’.

c. Product of ‘A’ and ‘C’ should not react with ‘B’.

d. Product of ‘A’ and ‘B’ should be ‘C’.

Question 4:  The titration in which an oxidizing agent is made to react with excess of solid KI and the  oxidizing agent oxidizes I^– to I₂ is known as

N₂(g) + 3H₂(g) →  2NH₃(g) ?

a. Iodometry

b. Iodimetry

c. Double titration

d. Back titration

Q.1	Q.2	Q.3	Q.4
b	a	d	a

Related Resources

• Look here for past year papers of IIT JEE  

• Click here to refer syllabus of chemistry for  IIT JEE