Chord of a Circle
A line that links two points on a circle is called a chord. Note that the end points of such a line segment lie on the circle. In fact, diameter is the longest chord.
The equation of the chord of the circle x2 + y2 + 2gx + 2fy +c=0 with M(x1, y1) as the midpoint of the chord is given by:
xx1 + yy1 + g(x + x1) + f(y + y1) = x12 + y12 + 2gx1 + 2fy1
i.e. T = S1
Methods of finding the length of the chord
There are two ways to find the length of the chord depending on what information is provided in the equation:
Given the radius and central angle
When the radius and a central angle are given, the length of the chord can be computed using the given formula:
Chord length = 2r sin (c / 2)
Where r is the radius of the circle and c is the angle subtended at the center
Given the radius and distance to center
In case, you are given the radius and the distance of the center of circle to the chord, you can apply this formula:
Chord length = 2√r2-d2 ,
where r is the radius of the circle and d is the perpendicular distance of the center of the circle to the chord.
There are various important results based on the chord of a circle. We discuss a few of them here as they often prove helpful in solving various questions.
Result: In case of intersection of two chords in the same circle, each chord gets divided into two segments by the other chord. The product of the segments of one chord is equal to the product of the segments of the other chord.
Result: Consider a circle with a tangent segment and a secant segment. Then the length of the tangent segment squared is equal to the product of the secant segment and its external segment.
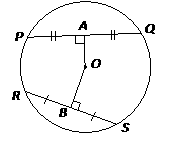
Result: A radius or diameter that is perpendicular to a chord divides the chord into two equal parts and vice versa.
In the above circle, if the radius OB is perpendicular to the chord PQ then PA = AQ.
Converse: The perpendicular bisector of a chord passes through the center of a circle.
In the above circle, OA is the perpendicular bisector of the chord PQ and it passes through the center of the circle. OB is the perpendicular bisector of the chord RS and it passes through the center of the circle.
Result: If two chords are congruent then they are equidistant from the center. The converse also holds true i.e. Chords equidistant from the center of a circle are congruent.
If PQ = RS then OA = OB or
If OA = OB then PQ = RS
For more, refer the video
Result: The arcs intercepted by two congruent chords are congruent.
Converse: If two arcs are congruent then their corresponding chords are congruent.
Illlustration:
If in the given circle with center O, the length of PQ is 10cm, then determine PA.
Solution:
As it is visible in the figure, OB is perpendicular to PQ. So, OB is a perpendicular bisector of PQ.
Hence, PA= ½ x PQ
= ½ x 10
= 5cm.
Illustration:
Find the equation of the circle whose center is (3, 4) and which touches the line 5x + 12y = 1.
Solution:
Let r be the radius of the circle. Then
r = distance of the center i.e. point (3, 4) from the line 5x + 12y = 1
= | (15+48-1)/√(25-44)|=62/13.
Hence the equation of the required circle is (x – 3)2 + (y – 4)2 = (62/13)2.
⇒ x2 + y2 – 6x – 8y + 381/169 = 0.
Illustration:
Find the co-ordinates of the point from which tangents are drawn to the circle x2 + y2– 6x – 4y + 3 = 0 such that the mid-point of its chord of contact is (1, 1).
Solution:
Let the required point be (P(x1, y1). The equation of the chord of contact of P with respect to the given circle is
xx1 + yy1 – 3(x + x1) –2(y + y1) + 3 = 0. … (1)
The equation of the chord with mid-point (1, 1) is
x + y – 3(x + 1) – 2(y + 1) + 3 = 1 + 1 – 6 – 4 + 3
⇒ 2x + y = 3.
Equating the ratios of the coefficients of x, y and the constant terms and solving for x1, y1 we get x1 = –1, y1 = 0.
In order to get an idea about the type of questions asked you may refer the Papers of Previous Years.
To read more, Buy study materials of Circles comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.