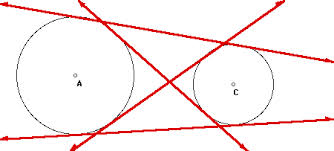
Common Tangents

 

Table of Content

Direct common tangents Important facts Transverse Common tangents What do we understand by co-axial circles and limiting points? When do two circles intersect orthogonally? Related Resources

There can be four common tangents to two circles. The tangents can be either direct or transverse.

When the two circles neither intersect nor touch each other, there are four common tangents.

But when they intersect there are two common tangents, both of them being direct.

Direct common tangents

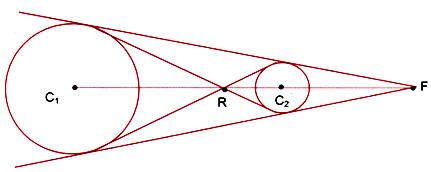
(i) The direct common tangents to two circles meet on the line of centres and divide it externally in the ratio of the radii. 

(ii) The transverse common tangents also meet on the line of centres and divide it internally in the ratio of the radii.

Important facts

• When one circle lies completely inside the other without touching, there is no common tangent. 

• When two circles touch each other internally 1 common tangent can be drawn to the circles. 

• When two circles intersect in two real and distinct points, 2 common tangents can be drawn to the circles. 

• When two circles touch each other externally, 3 common tangents can be drawn to the circles. 

• When two circle neither touch nor intersect and one lies outside the other, then 4 common tangents can be drawn. 

All this infromation along with the related conditions can be summarized as follows:

Number of Tangents                          Condition

4 common tangents                           r₁ + r₂ < c₁c₂

3 common tangents                           r₁ + r₂ = c₁c₂

2 common tangents                           |r₁ - r₂| < c₁c₂ < r₁ + r₂ 

1 common tangents                           |r₁ - r₂| = c₁c₂ 

no common tangents                         c₁c₂ < |r₁ - r₂| 

The lines represented in red in the figure given below are external common tangents and those represnted in blue are internal common tangents.

   

Note:

P is the point of intersection of two direct common tangents to the circles with centres C₁ and C₂ and radii r₁, r₂ respectively. C₁A₁, C₂A₂ are perpendiculars from C₁ and C₂ to one of the tangents (figure given below)    
∴ ΔPC₁A₁ and ΔPC₂A₂ are similar

(C₁P)/(C₂P) = (C₁ A₁)/(C₂ A₂ ) = r₁/r₂ i.e. P is a point dividing C₁C₂ externally in the ratio r₁ : r₂. For finding direct common tangents of two circles, find the point P dividing the line joining the centre externally in the ratio of the radii. Equation of direct common tangents is SS₁ = T₂ where S is the equation of one circle.
 

Transverse Common tangents 

P is the point of intersection of two transverse tangents to two non-intersecting circles with centres C₁ and C₂ and radii r₁, and r₂ respectively. Then P lies on the line joining the centres. C₁A₁ and C₂A₂ are perpendiculars from C₁ and C₂ to one of these tangents. (Figure given below) 

Since triangles C₁A₁P and C₂A₂P are similar. 
So (C₁ P)/(C₂ P)=(C₁ A₁)/(C₂ A₂ )=r₁/r₂ 
i.e. P divides the line joining C₁ and C₂ internally in the ratio r₁ : r₂ 
Equation of transverse Common tangents is SS₁ = T₂ where S is the equation of one of the circle.

Caution: 

Distance between the centres of two circles should be greater than sum of the radii of the circles to keep a possibility of transverse common tangent which is clear from the figure given above.

Note: 

Transverse tangents or Direct common tangents always meet on the line joining centres of the two circles. 

Remark:

Can we find the equation of the line joining the centres of two circles?

If S₁ = 0 and S₂ = 0 are two given circles, then S₁ – S₂ = 0 gives the equation of a line related to both of them. This line can give various results in varying conditions of relative positioning of two circles. 

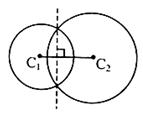
(i) Radical Axis of the two circles: Radical axis of the two circles is defined as the line from each point of which, tangents of equal length are drawn to the two circles. (see figure given below). 

In case of three circles radical point can be defined as the point where radical axis of three circles taken two at a time intersect. It is the point from which tangent of equal length can be drawn to all the three circles. 

If S ≡ x² + y² + 2gx + 2fy + c 
S’ ≡ x² + y² + 2g’x + 2fy’ + c’ 
Then equation of radical axis of two circles 
S = 0 and S’ = 0 is given by 
S = S’ 
i.e. x² + y² + 2gx + 2fy + c = x² + y² + 2g’x + 2f’y + c’ 
2(g – g’)x + 2(f – f’)y + (c – c’) = 0 
(ii) If the circles touch each other then the above equation gives the common tangent at the point where the circles touch each other. It is also the Radical axis of the two circles. 

(iii) If the two circles intersect then above equation gives the equation of the common chord. Here also the common chord is also the Radical axis of the two circles.

Note:

Two circles with centres C₁(x₁, y₁) and C₂(x₂, y₂) and radii r₁, r₂ respectively, touch each other. 

(i) Internally: If |C₁ C₂| = |r₂ – r₁| and the point of contact is ((r₁ x₂ - r₂ x₁)/(r₁+r₂ ) , (r₁y₂ - r₂y₁)/(r₁+ r₂)). 
(ii) Externally: If |C₁ C₂| = |r₂ – r₁| and the point of contact is ((r₁x₂ + r₂ x₁)/(r₁+ r₂) , (r₁ y₂+r₂ y₁)/(r₁+r₂)).
 

What do we understand by co-axial circles and limiting points? 

A system of circles every pair of which has the same radical axis is called a coaxial system. 

The centres of circles of a coaxial system, which are of zero radiuses, are called the limiting points o the coaxial system. 
Let the equation of a system of coaxial circles be 
x² + y² + 2gx + c = 0 
Where g is a parameter and c is a constant. 
It’s radius √(g²-c)and centre is (–g, 0) 
If g² – c = 0 or g = +√c, then radius become zero and for these two values of g we have two circles of zero radius whose centres are (± √c, 0). 

These circles of zero radius are just points and according to definition given above are the limiting points of the co-axial system. 

• If the system of circles is intersecting one, then c is negative and these limiting points are two imaginary points. 

• If the system of circles are non intersecting then c is positive and these limiting points are both real. 

• If c = 0, points of intersection are coincident to (0, 0) i.e.circle touch each other at (0, 0). Limiting points coincide at (0, 0). 
   

When do two circles intersect orthogonally? 

The angle of intersection between two curves intersecting at a point is the angle between their tangents drawn at that point. The curves are said to be intersecting orthogonally, if the angle between their tangents are common point is a right angle.

Consider two circles 

S₁ ≡ x² + y² + 2g₁x + 2f₁y + C₁ = 0 

S₂ ≡ x² + y² + 2g₂x + 2f₂y + C₂ = 0 

They intersect at point P such that tangent PT₁ and PT₂ are at right angle (see figure right side) 
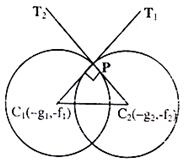Since radius of a circle is perpendicular to the tangent. So C₁P and C₂P are also perpendicular. 
⇒ (C₁C₂)² = (C₁P)² + (C₂P)² ⇒ (g₁ – g₂)² + (f₁ – f₂)² = r₁² + r₂² 
g₁² + g₂² – 2g₁g₂ + f₁² + f₂² – 2f₁f₂ = g₁² + f₁² – C₁ + g₂² + f₂² – c² 
⇒ 2g₁g₂ + 2f₁f₂ = C₁ + C₂ 
which is the required condition for the orthogonal intersection of two circles.

Illustration:

At what angle do the circles shown in figure intersect? 

From the triangle C₁C₂P it is clear that angle θ can be written as: 
cos θ = (r₁²+r₂²-d²)/(2r₁ r₂ ) 
Hence, this is the required angle.
 

Related Resources

• Click here to refer the most Useful Books of Mathematics.

• For getting an idea of the type of questions asked, refer the previous year papers.

• Fast Track your revision with the ultimate Revision Notes on Circle.

To read more, Buy study materials of Circles comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.