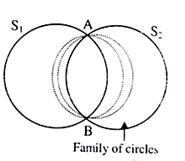
Family of Circles 

 

Table of Content

Introduction of Family of Circles Common chord of two circles Angle of intersection of two circles External and Internal Contacts of Circles  Related Resources

Introduction of Family of Circles

A collection of circles is called as a system or family of circles. There can be various types of family of circles

The general equation of a circle is x² + y² + 2gx + 2fy + c = 0. Since this equation involves three unknowns i.e. g, f and c so we need at least three conditions to get a unique circle.

For example, if we are given two circles and we want to determine the third circle touching both of them. We shall need one more condition. Without the condition we get the equation of family of circles which satisfies the two given conditions. Imposition of a third condition will result in the equation representing a particular circle. 

Let us now see some of the ways of finding the family of circles when certain conditions are given:

1. Family of circles having a fixed centre 

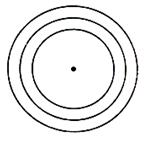This equation is given by (x – h)² + (y – k)² = r² (Figure given right)

Since (h, k) is fixed, so the only parameter varying is r. This is one parameter family of circles, and is the equation of the family of concentric circles. Fixation of the radius will give a particular circle. 

2. Equation of Family of circles passing through intersection of two circles S₁ = 0 and S₂ = 0. 

The general equation of the family of circles passing through the intersection of S₁ and S₂ in given by S₁ + kS₂ = 0, where k ≠ -1. Here again we have one-parameter (k) equation of family of circles. The particular value of the parameter gives a unique circle. 

Caution: 

If k = –1, we get equation of common chord i.e. straight line instead of circle. 

Let S₁ ≡ x² + y² + 2g₁x + 2f₁y + c₁ = 0 

S₂ ≡ x² + y² + 2g₂x + 2f₂y + c₂ = 0

Since, point lies on both the circles,

⇒ x_A² + y_A² + 2g₁x_A + 2f₁y_A + c₁ = 0

So, x_A² + y_A² + 2g₂x_A + 2f₂y_A + c₂ = 0

⇒ x_A² + y_A² + 2g₁x_A + 2f₁y_A + c₁ + λ (x_A² + y_A²  + 2g₁x_A + 2f₁y_A + c₁) = 0

⇒ Point A(x_A, y_A) lies on S₁ + λ S₂ = 0 ∀ λ ∈ R

Similarly point B(x_B, y_B) lies on S₁ + λ S₂ = 0 ∀ λ ∈ R

∴ S₁ + λ S₂ = 0 is the family of circles through the intersection of S₁ = 0 and S₂ = 0.

3. Equation of a circle circumscribing a triangle whose sides are given by L₁ = 0, L₂ = 0,  L₃ = 0.

This equation is given by L₁L₂  + λL₂L₃ + µL₃ L₁ = 0, provided coefficeint of xy = 0 and coefficient of x² = coefficient of y².

The particular value of the parameter λ and µ gives a unique circle. 

4. Family of circles touching the circle S = 0 and line L = 0 at their point of contact 

The required family is given by the equation S + λL = 0, where λ is the required family. 

5. Family of circle passing through two given points A(x₁, x₁) and B(x₂, y₂) 
 

 ∴ Required family of circles is 

6. Family of circles touching a given line L = 0 at a point (x₁, y₁) on the line is

(x – x₁)² + (y – y₁)² + λL = 0, the particular value of the parameters λ gives a unique circle.

The equation of the family of circles which touch the line y – y₁ = m (x – x₁) at (x₁, y₁) for any values of m is (x – x₁)² + (y – y₁)² + λ[(y – y₁) – m(x – x₁)] = 0. 

Here, we can have two sub-cases according as whether the line is parallel to x -axis or y-axis.

If this line through (x₁, y₁) is parallel to x-axis, then the equation of the family of circles touching it at (x₁, y₁) becomes (x – x₁)² + (y – y₁)² + K(y – y₁) = 0.

And if the line through (x₁, y₁) is parallel to x-axis, then the equation of the family of circles touching it at (x₁, y₁) becomes (x – x₁)² + (y – y₁)² + K(y – y₁) = 0.

7. Equation of circle circumscribing a quadrilateral whose sides in order are represented by the lines L₁ = 0, L₂ = 0,  L₃ = 0 and L₄ = 0 .

The equation of the required family is given by L₁L₃ + λL₂L₄ = 0, provided coefficient of x² = coefficient of y² and coefficient of xy = 0.
 

Common chord of two circles

The line joining the points of intersection of two circles is called the common chord. If the equations of the circles are

 S₁ ≡ x² + y² + 2g₁x + 2f₁y + c₁ = 0 

S₂ ≡ x² + y² + 2g₂x + 2f₂y + c₂ = 0, then the equation of the common chord is S₁ – S₂ = 0. 

Hence, the equation is 2x (g₁- g₂) + 2y (f₁-f₂) + c₁ – c₂ = 0.

Some key points:

• The length of the common chord is 2√(r₁² – p₁²) = 2√(r₂² – p₂²), where p₁ and p₂ are the length of perpendicular drawn from the centre to the chord.

• In the above equation of common chord, the coefficient of x² and y² in both the equations should be equal.

• Two circles touch each other if the length of their common chord is zero.

• The maximum length of the common chord is equal to the diameter of the smaller circle.
   

Angle of intersection of two circles

The angle of intersection between two circles S = 0 ans S’ = 0 is deifned as the angle between their tangents at their point of intersection.

If S =  x² + y² + 2g₁x + 2f₁y + c₁ = 0 

and S“ ≡ x² + y² + 2g₂x + 2f₂y + c₂ = 0, are two cricles with radii r₁, r₂ and ‘d’ is the distance between their centres then the angle of intersection θ between them is given by

cos θ = (r₁² + r₂² – d²)/ 2r₁r₂  or   cos θ = 2(g₁g₂ + f₁f₂) – (c₁ + c₂)/ 2√(g₁² + f₁² – c₁) √(g₂² + f₂² – c₂) 

Note: 

The two circles are said to intersect orthogonally if the angle of intersection of the circles i.e., the angle between their tangents at the point of intersection is 90^o. 

The condition for the two circles to cut each other orthogonally is 2gg₁+ 2ff₁ = c + c₁ where (–g, –f) and (–g₁, –f₁) are the centres of the respective circles, S = 0 and S₁ = 0. 

When two circles intersect orthogonally then the length of the tangent of one circle from the centre of other circle is equal to the radius of the other circle.
 

External and Internal Contacts of Circles 

A necessary and sufficient condition for the two circles to intersect at two distinct points is r₁ + r₂ > C₁C₂ > | r₁ - r₂|, where C₁, C₂ are the centres and r₁, r₂ be the radii of the two circles.

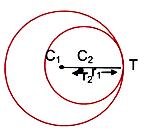
If two circles with centres C₁(x₁, y₁) and C₂(x₂, y₁) and radii r₁ and r₂ respectively, touch each other externally, C₁C₂ = r₁ + r₂. Coordinates of the point of contact are A ≡ ((r₁x₂+r₂x₁)/(r₁+r₂),(r₁y₂+r₂y₁)/(r₁+r₂)). 

The circles touch each other internally if C₁C₂ = r₁ + r₂.  

The circles touch each other internally if C₁C₂ = r₁ – r₂. 

Coordinates of the point of contact are 

T ≡ ((r₁x₂ - r₂x₁)/(r₁ - r₂),(r₁y₂ - r₂ y₁)/(r₁-r₂)).

Illustration: 

Examine whether the two circles x² + y² – 2x – 4y = 0 and  x² + y² – 8y – 4 = 0 touch each other externally or internally. 

Solution: 

Let C₁ and C₂ be the centres of the circles.

⇒ C₁(1, 2) and C₂(0, 4). Let r₁ and r₂ be the radii of the circles.

⇒ r₁ = √5 and r₂ = 2√5. Also C₁C₂ = √(1+4)=√5.

But r₁ + r₂ = 3√5 and r₂ – r₁ = √5 = C₁C₂.

Hence the circles touch each other internally.

Illustration: 

Find all the common tangents to the circles x² + y² – 2x – 6y + 9 = 0 and x² + y² – 6x – 2y + 1 = 0. 

Solution: 

The centres and the radii of the circles are 

C₁ (1, 3) and r₁ = √(1+9-9) = 1, C₂(–3, 1) and r₂ = √(9+1-1) = 3,

C₁C₂ = √20, r₁ + r₂ = 4 = √16 and C₁C₂ > r₁ + r₂.

Sense the circles are non-intersecting. Thus there will be four common tangents.

Transverse common tangents are tangents drawn from the point P which divides C₁C₂ internally in the ratio 1 : 3.

Direct common tangents are tangents drawn from the point Q which divides C₁C₂ externally in the ratio 1 : 3.

Coordinates of P are ((1(-3)+3.1)/(1+3),(1.1+3.3)/(1+3)) i.e. (0,5/2) and coordinates of Q are (3, 4).

Transverse tangents are tangents through the point (0,5/2).

Any line through (0,5/2) is y – 5/2 = mx …… (1)

⇒ mx – y + 5/2 = 0

Applying the usual condition of tangency to any of the circle, we get

(m.1 – 3 + 5/2 = 0)/√((m²+1) ) = 1 ⇒ (m-1/2)² = m² + 1

⇒ – m – 3/4 = 0 or 0.m² – m – 3/4 = 0.

⇒ m = –3/4 and ∞ as coefficient of m² is zero.

Therefore from (1),

(y-5/2)/x = m = ∞ and -3/4 ⇒ x = 0 is a tangent and 3x + 4y – 10 = 0 is another tangent.

Direct tangents are tangents drawn from the point Q(3, 4).

Now proceeding as for transverse tangents their equations are y = 4, 4x – 3y = 0.

Illustration: 

Find the equation of the circle described on the common chord of the circles x² + y² – 4x – 5 = 0 and x² + y² + 8y+ 7 = 0 as diameter 

Solution: 

Equation of the common chord is S₁ – S₂ = 0

⇒ x + 2y + 3 = 0

Equation of the circle through the two circles is S₁ + λS₂ = 0 

⇒ x² + y² -4/(1+λ ) x+8λy/(1+λ )+(7λ -5)/(1+λ ) = 0. 

Its centre (2/(1+λ ),-4/(1+λ )) lies on x + 2y + 3 = 0

⇒ 2/(1+λ )-8/(1+λ ) + 3 = 0 ⇒ 2 – 8λ + 3 + 3λ = 0 ⇒ λ = 1.

Hence the required circle is x² + y² – 2x + 4y + 1 = 0.

Illustration: 

The line Ax + By + C = 0 cuts the circle x² + y² + ax + by + c = 0 in P and Q. The Line A?x + B?y + C? = 0 cuts the circle x² + y² + a'x + b'y + c' = 0 in R and S. If P, Q, R, S are concyclic, prove that 

                                      

Solution: 

The equation of the circle through the first line and the first circle, i.e. through P and Q is 

x² + y² + ax + by + c + λ₁ (Ax + By + C) = 0. ........................ (1)

The equation of the circle through R and S is

x² + y² + a'x + b'y + c + λ₂ (A'x + B'y + C') = 0....................  (2)

Since P, Q, R, S are concyclic, (1) and (2) are identical.

⇒ 1 = (a+λ₁ A)/(a'+λ₂ A' )=(b+λ₁ B)/(b'+λ₂ B' )=(c+λ₁ C)/(c'+λ₂ C')

⇒ λ₁A-λ₂A' + a - a' = 0,

λ₁B -λ₂B' + b - b' = 0,

λ  ₁C-λ ₂C' + c - c' = 0. 

Illustration:  

Show that the circle passing through the origin and cutting the circles x² + y² - 2a₁x - 2b₁y + c = 0 and x² + y² - 2a₂x - 2b₂y + c = 0 orthogonally is 

                                    

Solution: 

Let the equation of the circle passing through the origin be 

x² + y² + 2gx + 2fy = 0. ..................... (1)

It cuts the given two circles orthogonally 

⇒ -2ga₁ - 2fb₁ = c₁ ⇒ c₁ + 2ga₁ + 2fb₁ = 0 ? (2)

and -2ga₂ - 2fb₂ = c₂ ⇒ c₂ + 2ga₂ + 2fb₂ = 0 ? (3) 
 

Illustration: 

Find the equation of the circle touching the line 2x + 3y + 1 = – at the point (1, -1) and is orthogonal to the circle which has the line segment having end points (0, -1) and (-2, 3) as the diameter.(IIT JEE 2004).

Solution: 

 The equation of the circle touching the line 2x + 3y + 1 = – at the point (1, -1) is 

(x-1)² + (y+1)² + λ(2x + 3y + 1) = 0

This gives x² + y² + 2x(λ-1) + y(3λ+2) + (λ+2) = 0 …. (1)

Now, this is orthogonal to the circle having end point of diameter (0, -1) and (-2, 3). 

This yields x(x+2) + (y+1)(y-3) = 0

i.e. x² + y² + 2x -2y -3 = 0 

Hence, 2(λ -2)/ 2. 1 + 2(3λ + 2)/ 2 (-1) = λ + 2-3

This gives λ -3/2

hence, from equation (1), we have the equation of circle as 2x² + 2y² – 10x – 5y +1 =0.

Illustration:

Find a circle passing through the intersection of x² + y² - 4 = 0 and x² + y² - 6x + 5 = 0 which passes through the point (2, 1)? 

Solution: 

Family of required circles is S₁ + λ S₂ = 0

⇒ (x² + y² - 4) + λ (x² + y² - 6x + 5) = 0 

Since the required circle passes through the point (2, 1), the previous equation is satisfied for the point (2, 1) 

⇒ (4 + 1 - 4) + λ (4 + 1 - 12 + 5) = 0

1 - 2λ = 0 ⇒ λ = ½

∴ Equation of the required circle is

(x² + y² - 4) + 1/2 (x² + 2y - 6x + 5) = 0

⇒ x² + y² - 2x - 1 = 0
 

Related Resources

• Click here to refer the most Useful Books of Mathematics.

• For getting an idea of the type of questions asked, refer the previous year papers.

• Fast Track your revision with the ultimate Revision Notes on Circle.

To read more, Buy study materials of Circles comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.