Working Rule for finding the Area
|
(ii) If curve lies on both the sides of x axis i.e. above the x axis as well as below the x axis, then calculate both areas separately and add their modulus to get the total area. In general if curve y = f(x) crosses the x axis n times when x varies from a to b, then the area between y = f(x), x axis and lines x = a and x = b is given by A = |A1| + |A2| + ... + |A11| |
|
(iii) If the curve is symmetrical about x axis, or y axis, or both, then calculate the area of one symmetrical part and multiply it by the number of symmetrical parts to get the whole area.
Illustration 15 Find the area between the curves y = x2 + x –2 and y = 2x, for which |x2+ x –2| + | 2x | = |x2 + 3x –2| is satisfied.
|
Solution: y = x2 + x - 2 => y = 2x |x2 + x - 2| + |2x| = |x2 + 3x -2| (x2 + x - 2) and 2x have same sign Thus required area ar (PQR) + ar (ECD) = ∫0–1 [2x - (x2 + x - 2)] dx + ∫21 [2x - (x2 + x - 2)] dx = [x2/2 – x3/3 + 2x]0–1 + [x2/2 – x3/3 + 2x]21 = 7/6 + [10/3 –13/6] = 7/6 + 7/6 = 7/3 |
|
Illustration 16 Find out the area enclosed by circle |z| = 2, parabola y = x2 + x + 1, the curve y = [sin2 x/4 + cos x/4] and x-axis (when [ . ] is the greatest integer function).
Solution:
For x ∈ [-2, 2]
=> 1 < sin2 x/4 + cos x/4 < 2
∴ [sin2 x/4 + cos x/4] = 1
Now we have to find out the area enclosed by the circle |z| = 2,
parabola (y - 3/4) = (x+1/2)2,
line y = 1and x-axis.
∴ Required area is shaded area in the figure.
Hence required area = √3 × 1 + (√3 – 1) + ∫01 (x2 + x + 1).dx + 2 ∫2√3√4–x2 dx
= (2π/3 + √3 – 1/6) sq. units
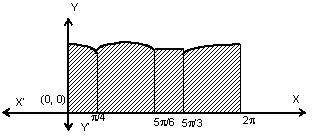
Illustration 17: Let f(x) = Max. {sinx, cos x, 1/2} then determine the area of the region bounded by the curves y = f(x), x-axis, y-axis and x = 2π.
Solution:
f(x) = Max {sin x, cos x, 1/2}
interval value of f(x)
for 0 < x < π/4, cos x
for π/4 < x < 5π/6, sin x
for 5π/6 < x < 5π/3, 1/2
for 5π/3 < x < 2π cos x
Hence required area
= ∫π/40 cosx dx + ∫5π/6π/4 sin x dx + ∫5π/35π/6 1/2.dx + ∫2π5π/3 cosx dx
= (5π/12 + √2 + √3) sq units.
Illustration 18: Find area bounded by y = |4 – x2|/4 and y = 7 - |x|
Solution:
y = |4 – x2|/4 (I)
y = 7 – |x| (II)
Rewriting (I) and (II)
|
y = {4–x2 / 4 – 2< x < 2 x2–4/4 x∈(–∞, –2) U (2, ∞) y = {7 – x x >0 7 + x x < 0 Required area (PQRSTUP) = 2 area (PQRSP) = 2 [area of (OVRSO) – area of (POQP) – area of (QRVQ) ] |
|
= 2 [1/2 (7 + 3)4 - ∫20 (4–x2/4) dx – ∫42 x2–4/4 dx]
= 2 18 + 2/3 – 16/3 + 4 + 2/3 – 2
= 32 sq unit.
Illustration 19: Let f be a real valued function satisfying f(x/y) and limx–>0 f(1+x)/x = 3. Find the area bounded by the curve y = f(x), the y axis and the line y = 3
Solution:
Given = f(x/y) = f(x) – f(y) .... (1)
Putting x = y = 1, we get f(1) = 0
Now, f’(x) = limh–>0 f(x+h) – f(x) / h
= Limh–>0 f(1+h/x)/h (from(1))
= Limh–>0 f(1+h/x) (h/x)x
=> f'(x) = 3/x {since Limx–>0 f(1+x0/x = 3}
=> f(x) = 3 ln x + c
Putting x = 1
=> c = 0
=> f(x) = 3 ln x = y (say)
Required area = ∫3–∞ x dy = ∫3–∞ ey/3 dy = 3[ey/3]3–∞
= 3 (e – 0) = 3e sq. units
Illustration 20: Let An be the area bounded by y = tann x, x =0, y = 0 and x = p/4. Prove that for n ³ 2. (i) An+An-2 = 1/n–1 (ii) 1/2(n+1) < An < 1/2(n–1)
|
Solution: (i) Obviously An = .∫π/40 tann xdx An+An–2 = ∫π/40 (tann xdx + tann–2x)dx =∫10 tn–2 dt = 1/n–1. |
|
(ii) Obviously An+2< An< An-2 (from figure).
Thus 2 An = An + An < An + An-2 = 1/n–1 (by part (i)
Thus An < 1/2(n–1) . . . . (1)
Also 2 An = An+ An > An + An+2 = 1/n+1, replacing n by n+2 in (i)
An > 1/2(n+1) . . . . (2)
From (1) and (2), we get 1/2(n+1) < An < 1/(2n–1).
To read more, Buy study materials of Definite integral comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.