Introduction to Differentiation

 

Table of Content

Introduction to Differentiation Differentiation as a slope of the curve Related Resources

Introduction to Differentiation

The derivative is the instantaneous rate of change of a function with respect to one of its variables. 

Differential coefficient of a function y = f(x) is written as d/dx [f(x)] or f'(x) or f⁽¹⁾(x) and is defined by

f'(x) = lim _h→0 (f(x+h) – f(x))/h

f'(x) represents nothing but ratio by which f(x) changes for small change in x and can be understood as

f'(x) = lim _?x→0 ((?y)/(?x)) = dy/dx

Thus, f’(x) which is called as the derivative of x basically represents or denotes the rate of change of y with respect to x. The derivative f’(x) also represents the slope of the tangent drawn at a point x of the curve f(x). 

Having discussed the meaning of differentiation, we now discuss the geometrical interpretation of differentiation:

Slope of PQ = (y_Q - y_p)/y_Q

                = ((y + ?y) – y)/((x + ?x) – x) or (f(x + ?x) – f(x))/((x + ?x) – x)

                = ?y/?x

                = (f(x + ?x) – f(x))/?x

Let the point Q approach point P in the curve y = f(x) i.e. ?x → 0.

Then, we observe graphically that the slope of chord PQ becomes the slope of the tangent at the point P which is written as dx/dy or f'(x).

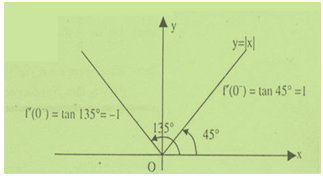
Since, point Q is approaching point P from the Right Hand side, we obtain f'(x⁺) as follows:

f'(x⁺) = lim _?x→0 (f(x + ?x) – f(x))/?x

This is termed as the Right Hand Derivative. Similarly, we can have

f'(x^-) = lim _?x→0 (f(x + ? x) – f(x))/(-?x), ?x > 0

This is termed as the left hand derivative. 

Remark:   For a function to be differentiable at the point x = a, we must have the left hand derivative equal to the right hand derivative, i.e. f'(a-) = f'(a+) i.e. lim h→0 (f(a – h) – f(a))/(-h) = lim h→0 (f(a + h) – f(a))/h From the above graphs, one must not infer that a curve is non-differentiable only at points of discontinuity. Non differentiability conditions also arise when the curve is continuous and the curve suddenly changes direction.

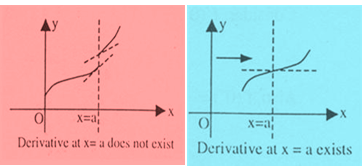
One can also judge the existence of derivative of a function by simply drawing its graph. The graph of a function directly helps you identify whether the derivative at a point exists for a function or not. 

The following two graphs clearly indicate how to identify whether the derivative of a function exists at a point or not:

The easiest example of a curve being continuous and non-differentiable is y = |x| at x = 0. However, when there is a smooth change or gradual change in slope or trajectory of a curve, the derivative exists.

We now try to throw some light on the concept of differentiation with the help of some graphs:

	In the adjoining figure, we can see that the derivative of the function f(x) i.e. f'(x) exists at ‘a’ i.e. f'(a) exists and is finite.
	The figure clearly shows that both f'(a-) and f'(a+) exist but they are not equal and hence the function is not differentiable.
	It is apparent by the figure that the function has infinite derivative.
	The adjoining figure clearly shows that the function has infinite derivative.
	The figure shows that the function has infinite derivative and f'(a-) = +∞ and f'(a+) = - ∞ and hence f'(a) does not exist.

  Note: 

Differentiability implies continuity but continuity does not imply differentiability.

If a function is differentiable, then it is obviously continuous but the continuity of a function does not guarantee its differentiability.
 

Differentiation as a slope of the curve

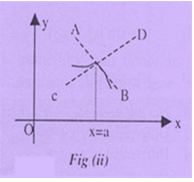
Let us first plot the graph of a function y = f(x) and then we draw a tangent to the curve at point A whose co-ordinates are (x₁, y₁). Select a neighboring point B whose co-ordinates are (x₂, y₂), such that (x₂ - x₁) = Δx and y₂ - y₁ = Δy. AB is a straight line segment which does not overlap with the portion of the curve cut by it. As point B approaches Δy approaches 0) the portion of the curve between AB can be approximated (to remarkable accuracy) as a straight line segment which overlaps with line segment AB. Thus in the limit Δx approaches 0 the line segment AB extended (or line passing through AB) is called tangent to the curve at point A.

As a matter of curiosity let us look what is the angle θ the tangent line to the curve at A makes with x-axis

tan θ lim _x2→x1 (y₂ - y₁)/(x₂ - x₁) = lim _{Δx →0} ?y/?x = dy/dx |_A

As Δx approaches 0 (mathematically denoted as Δx → 0) the difference between x₂ and x₁ become infinitesimal represented by dx.

tan θ = lim _{Δx → 0} ?y/?x = dy/dx

The value of tan θ is called slope of the curve at point A. If the slope of curve at all points is same, the curve is a straight line. The slope at a point on the curve gives information regarding bending of the curve.

Now if y is a function of x then dy/dx or d/dx of y is called derivative of y with respect to x or differentiation of y with respect to x is also denoted by f'(x), that is dy/dx = f'(x) = y₂ - y₁.

Physically dy/dx represents the ratio of infinitesimally small change in y to that of corresponding change in x. In other words dy/dx is called the rate of change of y with respect to x or differential coefficient of a function with respect to x.

Q1. Instantaneous rate of change of a function with respect to one of its variables is called

(a) differentiation

(b) integration

(c) factorial

(d) summation

Q2. A curve is non-differentiable only at points of 

(a) discontinuity

(b) continuity

(c) is always differentiable

(d) not only at points of discontinuity but may be at points of continuity as well.

Q3. Curve which is continuous and non-differentiable is 

(a) y = x at x = 0

(b) y = |x| at x = 0

(c) fy = – x at x = 0

(d) y = |x| at x = 1

Q4. The relation between continuity and differentiability is

(a) they are not related to each other.

(b) it is a two-way relationship.

(c) Differentiability implies continuity but continuity does not imply differentiability

(d) Continuity implies differentiability but differentiability does not imply continuity

Q5. In case of a curve where there is a smooth change or a gradual change, 

(a) the integral exists.

(b) integral and derivative both exist.

(c) the derivative does not exist.

(d) the derivative exists.

Q1.	Q2.	Q3.	Q4.	Q5.
(a)	(d)	(b)	(c)	(d)

Related Resources

• You may wish to refer Limits using Differentiation.

• Click here to refer the most Useful Books of Mathematics.

• For getting an idea of the type of questions asked, refer the previous year papers.

To read more, Buy study materials of Methods of Differentiation comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.