Second Order Derivative
Table of Content |
|
|
First Derivative
First Derivative is the slope of the tangent line to the function at the point x.
Notation
If the function is f(x) then its derivative will be written as:

Formula
Its formula to find the first derivative is

Example
Derivate the function f(x) = x2
Solution:
Given f(x) = x2,
So f(x + Δx) = (x + Δx)2
Now expand (x + Δx)2
f(x + Δx) = x2 + 2x Δx + (Δx)2
As we know the formula of slope is

Put the values of f(x + Δx) and f(x) in formula

And then as Δx heads towards 0 we get Δy/Δx = 2x
Hence the derivative of x2 = 2x
What is the derivative of zero?
As the derivative of constant is always zero, so the derivative of zero is also zero because 0 is also a constant.
All the constants has horizontal line either it is y = 5 or y = 0, this shows that all the constants have constant slope.
Limit definition of derivative:

Zero is a function of x such that
f(x) = 0 ∀ x
So f(x + h) = f(x) = 0

What does the first derivative tells us?
The first derivative tells us whether the function is increasing or decreasing due to change and by how much.
-
The positive slope shows that f(x) increases with increase in x.
If dy/dx > 0, then f(x) is an increasing function at x = a.
-
The negative slope shows that f(x) decreases with increase in x.
If dy/dx < 0, then f(x) is a decreasing function at x = a.
-
Zero slopes do not show anything in particular.
If dy/dx (α) = 0, then x = a is called a Critical Point of f(x), and it does not show anything about the behavior of f(x) at x = a.
 |
 |
First Derivative Test
A point (x, y) on the graph of a function at which the derivative is either 0 or undefined is called critical point. It will be a minimum or maximum.
For a given Critical Point:
-
If the derivative is negative on the left of the critical point and positive on the right, then this shows that the critical point is a minimum.
-
If the derivative is positive on the left of the critical point and negative on the right, then this shows that the critical point is a maximum.
-
In any other case, the critical point is neither minimum nor maximum.
Example
If we have a function f(x) = 6x – x2, then its fꞌ(x) = 6 – 2x
When we solve it as equation then x = 3, so f has a critical point at x = 3
Now when we consider where f is increasing and decreasing, we got to know that x = 3 is a maximum.
Second Order Derivative
Second Derivative of a function is the derivative of the first derivative.so first we will find the first derivative then take its derivative again to find the second derivative.
Notation
The Second Derivative of function f(x) is represented as:
Power Rule
To find the second derivative we have to apply the power rule to find the first derivative and then apply again to find the second derivative.
If f is a function such that f(x) = xa and f is differentiable at x then,
fꞌ(x) = axa-1
To find the second derivative we will use the power rule again.
fꞌꞌ(x) = a (a-1)xa-2
What does the second derivative tells us?
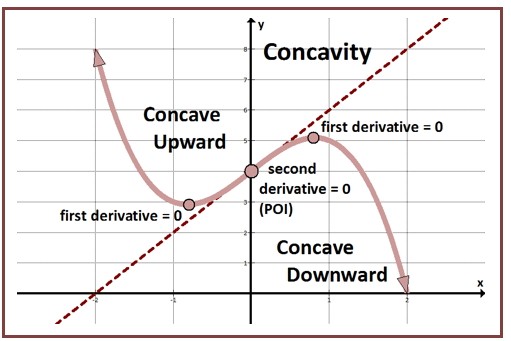
As the first derivative tells us that the function is increasing or decreasing, the second derivative tells us that the function is concave up or concave down.
-
If the second derivative of a function is positive then this shows that the function is concave up (U) that is, the slope of the tangent line to the function is increases with increase in x .
If d2y/dx2 (p) > 0 at x = p, then f(x) is concave up at x = p
- If the second derivative of a function is negative then this shows that the function is concave down (∩) that is, the slope of the tangent line to function is decreases with increase in x.
If d2y/dx2 (p) < 0 at x = p, then f(x) is concave down at x = p.
-
if the second derivative of a function is zero, then the function could be concave up or concave down or it may be shifting from concave up to concave down or vice versa.
If d2y/dx2 (p) = 0 at x = p, then it doesn’t tell anything about the slope of f(x) at x = p.
Point of Inflection (POI)
The Inflection Point is a point on the graph of the function where the graph changes from concave up to concave down or vice versa. The second derivative changes sign at this point from positive to negative or viceversa.the second derivative of the function is zero at this point.as it is shown in the above figure as POI.
Second Derivative Test
We use the second derivative test to check, when x is local maximum or local minimum.
-
If the first derivative is zero and the second derivative is positive, then the derivative of f(x) is increasing at that point that is, the curve is concave up at that point. Hence x is local minimum of function f(x).
If dy/dx (p) = 0 and d2y/dx2 (p) > 0, then f(x) has a local minimum at x = p.
-
If the first derivative is zero and the second derivative is negative, then the derivative of f(x) is decreasing at that point taht is, the curve is concave down at that point. Hence x is local maximum of function f(x).
If dy/dx (p) = 0 and d2y/dx2 (p) < 0, then f(x) has a local maximum at x = p.
-
If the first derivative is zero and the second derivative is also zero then the point x could be local maximum or local minimum and the function could be increasing or decreasing at that point.
If dy/dx (p) = 0 and d2y/dx2(p) = 0, then we cannot tell about the movement of f(x) at x = p.
Example
Find the critical point of f(x) = x 3 − 9x 2 + 15x – 7 and if any of the critical point is local minimum or local maximum.
Solution:
First of all we have to solve for the first derivative of the function.
f(x) = x 3 − 9x 2 + 15x – 7
fꞌ(x) = 3x2 – 18x + 15
Now to find the critical point, we will solve it by putting it equal to zero as the critical point is the value of x when the first derivative of f(x) is zero.
3x2 – 18x + 15 = 0
x2 – 6x + 5 = 0 (by dividing both sides with 3)
(x – 1)(x – 5) = 0
x = 1 or x = 5
So the critical points of f(x) are x = 1 and x = 5.
Now we will find the second derivative to check that at these critical points the f(x) is local maximum or local minimum.
fꞌꞌ(x) = 6x – 18
Check with the second derivative test at the given critical points.
Second Derivative of f(x) at x = 1 is
fꞌꞌ(x) = 6x – 18
= 6(1) – 18
= -12
Second Derivative of f(x) at x = 5 is
= 6(5) – 18
= 30 – 18
= 12
Hence, the above test shows that the f(x) has local maximum at x = 1 as the fꞌꞌ(x) is negative and the f(x) has local minimum at x = 5 as the fꞌꞌ(x) is positive.
What is the first derivative of distance?
Distance is the path on which you have moved and speed is the ratio which shows that how much distance you have covered in particular time. So, the formula of speed is:
This is actually the first derivative of distance over time. If distance is‘s’ and time is‘t’ then we can write the first derivative of speed as:

If a person is covering 20m in 2 sec then the speed will be 10m/s.
Is the Second Derivative acceleration?
if we start moving fast, then the speed will increase. When the speed is accelerating then the first derivative is changing over time.
So that we will find the second derivative to calculate the increase in speed.
If the speed is increasing from 20m to 24 m for next 2 seconds then the second derivative will be

This shows that acceleration is the second derivative.
Graph of a function and its derivatives
If there is a function f(x) = -4x2 + 3x then we can draw the graph by solving it as equation.
f(x) = -4x2 + 3x
= x (-4x + 3)
x = 0 and x = 3/4
Here the red color graph is for function f(x) = -4x2 + 3x
fꞌ(x) = – 8x + 3
x = 3/8
The blue color graph is for its first derivative fꞌ(x) = -8x +3
fꞌꞌ(x) = – 8
y = – 8
The green color graph is for the second derivative fꞌꞌ(x) = – 8
More Readings