Tangents and Normal

 

Table of Content

Introduction to Tangents and Normal Some Important Points Some Common Parametric Coordinates on a Curve Angle of Intersection of two Curves Length of the Tangent, Normal, Subtangent and Subnormal Interpretation of dy/dt as a rate measure Test your knowledge

Introduction to Tangents and Normal

Tangents and Normal is the introducing part in the Application of Derivatives. The chapter starts with basic concepts of equations of tangent and normal to general curves, angle of intersection between two curves and goes on to discuss more fundamental concepts. The concepts have been explained in detail along with various illustrations and figures (wherever necessary).

"Tangents and Normal" is one of the scoring topics of Differential Calculus in the Mathematics syllabus of IIT JEE, AIEEE and other engineering examinations. It requires a good understanding of graphs and further helps in the portion of Coordinate Geometry, another important unit in the syllabus.

The tangent to the curve y = f(x) at the point (x, y) makes an angle Ψ with the positive x-axis. Then dy/dx = tan Ψ. Thus the derivative dy/dx or f'(x) represents the slope of the tangent to the curve at the point (x, y).

Equation of normal at (x₁, y₁)

   where the slope is calculated at the point (x₁, y₁)

In some cases, dy/dx fails to exist but even then a tangent can be drawn.

Let us discuss these concepts with the help of an example:

PT is the tangent to the curve y = f(x) at the point P(x₁, y₁).

PN is the normal to the curve at P.

The slope of the tangent at P(x₁, y₁) is, [dy/dx]_(x1,y1).

The slope of the normal at P(x₁, y₁) is, -1/[dy/dx]_(x1,y1).

Hence the equation of the tangent PT is, y - y₁ = [dy/dx]_(x1,y1) (x - x₁),

and the equation of the normal PN is, y - y₁ = -1/[dy/dx]_(x1,y1) (x - x₁)

If (dy/dx)_(x1,y1) = 0, then the equation of the normal would be x = x₁.

If the equation of the curve is in the parametric form x = f(t) and y = g(t),

Then dy/dx = dy/dt/dx/dt = (g' (t))/(f' (t)).

Thus the equations of the tangent and the normal are

y - g(t) = (g' (t))/(f' (t)) (x - f(t))

and  f'(t)[x - f(t)] + g'(t)[y - g(t)] = 0.
 

Some Important Points

• If dy/dx at (x₁, y₁) = 0 then the tangent is parallel to x-axis and conversely.

• If the tangent is parallel to ax + by + c = 0 then dy/dx = -a/b

• If dy/dx at (x₁, y₁) → ∞ i.e. dx/dy at (x₁, y₁) = 0 then the tangent is perpendicular to x- axis.

• If the tangent at P(x₁, y₁) is equally inclined to the coordinate axes, then dy/dx at (x₁, y₁) = ± 1.

• If the tangent makes equal non-zero intercepts on the coordinate axis, then dy/dx at (x₁, y₁) = -1.

• If the tangent cuts off from the coordinate axis equal distance from the origin then dy/dx = ±1.
   

Some Common Parametric Coordinates on a Curve

• For x^2/3 + y^2/3 = a^2/3, assume the parametric coordinates x = a cos³θ and y = a sin³θ .

• For √x + √y = √a, assume x = cos⁴θ and y = a sin⁴θ

• For xⁿ/aⁿ + yⁿ/bⁿ = 1, assume x = a (sin θ)^2/n and y = b(sin θ)^2/n.

• For y² = x³, take x = t² and y = t³.
   

Angle of Intersection of two Curves

The angle of intersection of two curves at a point P is defined as the angle between the two tangents to the curve at their point of intersection.

Let there be two curves y = f₁(x) and y = f₂(x) which intersect each other at point (x₁, y₁). If we draw tangents to these curves at the intersecting point, the angle between these tangents is called the angle between two curves.

Let m₁ = (df₁(x))/dx |_{(x = x1)} and m₂ = (df₂(x))/dx |_{(x = x1)}

And both m₁ and m₂ are finite.

The acute angle between the curves is given by

θ = tan^-1 |(m₁ – m₂)/(1 + m₁ m₂)|

  Note:  (p - q) is also an angle between lines.

If m₁ (or m₂) is infinity the angle is given by θ = |π/2 – θ₁| where

θ₁ = tan^-1 m₂ (or tan^-1 m₁)

In the figure given below, Φ is the angle between the two curves,which is given by

Φ = Ψ₁ - Ψ₂

⇒ tan Φ = tan (Ψ₁ - Ψ₂)

= (tan Ψ₁ – tan Ψ₂)/(1 + tan Ψ₁ tan Ψ₂ ), where tan Ψ₁ = f'(x₁) and tan Ψ₂ = g'(x₁).

Two curves are said to cut each other orthogonally if the angle between them is a right angle, in which case we will have,

tanΨ₁ tanΨ₂ = -1.

Two curves touch each other if the angle between the tangents to the curves at the point of intersection is 0^o, in which case we will have,

tanΨ₁ = tanΨ₂.
 

Illustration:

Show that the curves ax² + by² = 1 and cx² + dy² = 1 cut each other orthogonally if, 1/a – 1/b = 1/c - 1/d.

Solution:

Let the two curves cut each other at the point (x₁, y₁). Then

ax₁² + by₁² = 1                                                           ...... (1)

and cx₁² + dy₁² = 1.                                                     ...... (2)

From (1) and (2), we get

(a - c)x₁² + (b - d)y₁² = 0.                                           ...... (3)

Slope of the tangent to the curve ax² + by² = 1, at (x₁, y₁) is given by

tan Ψ₁ = [dy/dx]_(x1,y1) = -ax₁/by₁ .

Slope of the tangent to the curve cx² + dy² = 1 at (x₁, y₁) is given by

tan Ψ₂ = [dy/dx]_(x1,y1) = -cx₁/dy₁. If the two curves cut orthogonally, we must have,

(-ax₁/by₁)(-cx₁/dy₁) = -1 ⇒ acx₁² + bdy₁² = 0.                          ...... (4)

From (3) and (4) we have

(a-c)/ac = (b-d)/bd ⇒ 1/a – 1/c = 1/c – 1/d.

Illustration 2:

Prove that the tangent lines to the curve y² = 4ax at points where x = a are at right angles to each other.

Solution 2:

y² = 4ax

When x = a

y² = 4a²

⇒ y = ± 2a

Points are (a, 2a) and (a, - 2a)

Slope of the tangent of the curve y² = 4ax is

y dy/dx = 4a

dy/dx = 2a/y

for y = 2a, dy/dx = 1 = m₁

for y = -2a dy/dx = - 1 = m₂

m₁m₂ = -1
 

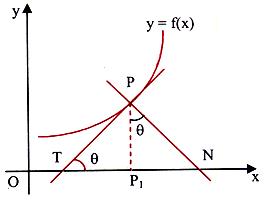
Length of the Tangent, Normal, Subtangent and Subnormal

Let P(x, y) be any point on y = f(x). Let the tangent drawn at 'P' meet the x-axis at 'T', and normal drawn at 'P' meets the x-axis at 'N'. PT is called the length of the tangent and PN is called the length of the normal.

If 'P₁' be the projection of the point P on the x-axis then TP₁ is called the sub-tangent (projection of line segment PT on the x-axis) and NP₁ is called the sub normal (projection of line segment PN on the x-axis).

Tangent:

TP = PP₁ cosec θ = y √(1 + cot²θ)

  =

Subtangent:

TP₁ = PP₁ cot θ

=

Normal:

PN = PP₁ sec θ = y √(1 + tan²θ)

=

Subnormal:

NP₁ = PP₁ tan y = |y(dy/dx)|
 

Interpretation of dy/dt as a rate measure

We know that by the derivative dr/dt, we mean the rate of change of distance r with respect to time t. In the similar way, when some quantity y varies or changes with some other quantity x while satisfying some rule y = f(x), then the derivative dy/dx i.e. f’(x) implies the rate of change of y with respect to x. 

Let us discuss some of the solved examples based on these concepts:

Example 1:

The coordinates of the feet of normals drawn from the point (14,7) to the curve y² - 16x – 8y = 0 are

(a) (0,0)                     (b) 3,2)                          (c ) (3,-4)               (d) (8, 16)

Solution

Given curve is y² - 16x – 8y = 0                       ….… (1)

Let P = (14, 7)

Then equation (1) can be written as y² – 8y = 16x

or y² – 8y + 16 = 16x + 16

Or (y – 4)² = 16(x + 1)                                ….….…. (2)

This is of the form (y –l)² = 4a(x-s), where a = 4, s = -1, l = 4.

Let (-1+4t², 4+8t) be any point on the curve (2).

Then from (2) , we have 2(y-4) dy/dx = 16.

Hence, dy/dx = 8/(y-4)

at (4t² – 1, 4 + 8t), dy/dx = 1/t

Hence, the equation of normal at (-1 + 4t², 4+8t) is

y - 4 – 8t = – t(x + 1 – 4t²)

or tx + y – 4 – 8t + t – 4t³ = 0 ….….. (3)

If line passes through the point P(14, 7) then

14t + 7 – 4t³ – 7t – 4 = 0

or 4t³ – 7t -3 = 0

(t + 1)(4t² – 4t – 3) = 0

Hence, t = -1, (4 ± 8)/8 = -1, 3/2 , -1/2.

when t = -1, foot of the normal is (3, -4)

when t = 3/2, foot of the normal is (8, 16)

when t = -1/2, foot of the normal is (0, 0).

Example 2

Find the equations of the tangents to the curve x² + y² – 2x – 4y + 1 = 0 which are parallel to the x-axis.

Solution

The equation of the curve is x² + y² – 2x – 4y + 1 = 0.

Hence, 2x + 2y dy/dx – 2 – 4 dy/dx = 0

So, (2y – 4) dy/dx = 2 – 2x

Hence, dy/dx = (2 – 2x)/(2y - 4) = (1 – x)/(y – 2)

Since the tangents are parallel to the x- axis, so the slope of each of the tangent is zero.

Hence, (1 - x)/(y – 2) = 0

So, x = 1.

At x = 1, 1² + y² – 2(1) – 4y + 1 = 0

So, y² – 4y = 0

this gives y = 0 or y = 4.

Therefore, the points are (1,0) and (1,4).

Hence, the equation of tangent through (1, 0) and parallel to the x-axis is y = 0 and the equation of tangent through (1, 4) and parallel to the x-axis is y = 4.

Hence, the required equations of the tangents are y = 0 and y = 4.

 

Q1. If the curves are orthogonal, then

(a) (dy₁/dx)(dy₂/dx) = -1

(b) (dy₁/dx)(dy₂/dx) = 1

(c) (dy₁/dx)(dy₂/dx) = 0

(d) (dy₁/dx)² = -1

Q2. If θ is the angle between y = x² and 6y = 7-x³ at (a, a) then θ is:

(a) 2π

(b) π

(c) π/3

(d) π/2

Q3. If F(x) = f(x).g(x) are such that f(x) is continuous at x = a and g(x) is differentiable at x = a with g(a) = 0 then the product function f(x).g(x) is

(a) continuous at x = a

(b) differentiable at x = a

(c) can’t say

(d) may or may not be differentiable at x = a

Q4. If the curves ay + x² = 7, a > 0 and x³ = y cut orthogonally at (1,1), then a = ?

(a) 4

(b) 1/2

(c) 6

(d) 2

Q5. If the value of dy/dx at the point (x₁,y₁) and exists and is 0, then

(a) tangent is parallel to x-axis.

(b) tangent is perpendicular to x-axis.

(c) tangent may or may not be parallel to x-axis.

(d) can’t say

Q1.	Q2.	Q3.	Q4.	Q5.
(a)	(d)	(b)	(c)	(a)

The chapter is important not only because it fetches 2-3 questions in most of the engineering examination but also because it is a helping hand in the unit of Coordinate Geometry.Tangents and Normal is an important chapter in Differential calculus. It is considered to be marks fetching as the Multiple Choice Questions that are framed on this topic are direct and simple. You are expected to do all the questions based on this to take an edge in IIT JEE examination. It is very important to master these concepts as this forms a strong base of your preparation for IIT JEE, AIEEE, DCE, EAMCET and other engineering entrance examinations. 

To read more, Buy study materials of Applications of Derivatives comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.