De-Broglie Waves

Classical physics predicts electron should “spiral in” to the nucleus emitting continuous spectrum of radiation as the atom “collapses”. Classical physics can’t give us stable atoms.

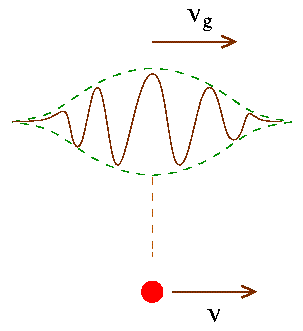
In 1924, the French physicist Louis de Broglie proposed that moving objects behave like waves; these are called Matter Waves.

De Broglie waves represent the set of waves which establish or reveal the nature and conduct of some atoms, molecules or some elementary particles under certain circumstances.

The de Broglie Wavelength is denoted by λ and is written as,

Here the symbols have the following meanings.

‘h’ stands for Planck constant

‘m’ denotes the mass

‘v’ is the velocity of the particle

So, the momentum of ‘p’ will be,

Hence, the De Broglie relation shows that the wavelength is proportional to the momentum of the particle. The frequency of the waves has also been deduced by Broglie and he has proved it to be directly proportional to the total energy E of the particle(where E is the sum of potential and kinetic energy).

The French Physicist Louis de Broglie, in 1924 suggested that besides the particle properties, particles may also exhibit wave properties. It took around three years to spot the wave nature of electrons. These waves are also called as matter waves and they demonstrate the properties of a material object which tend to change in time or space in accordance with the mathematical equations which illustrate these waves. De Broglie waves play a vital and commendable role but only in the case of subatomic particles.

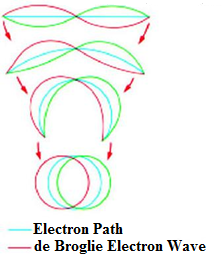
An electron can circle a nucleus only in orbits that contain a whole number of de Broglie Wavelengths. The quantum number n of an orbit is the number of electron waves that fit into the orbit.

It is only due to the Broglie waves that subatomic particles can be found in otherwise unexpected cases. The reason behind this is the ability of these waves to penetrate barriers.      

The Broglie waves around a closed loop just like the waves coupled with electrons attached to the nuclei in atoms can continue to stay provided the waves fit perfectly around the loop, else they cancel out themselves. It is this necessity that forces the electrons in atoms to opt for some specific structures or arrangements out of the many which would have been there otherwise. 

It was in 1925, even before the discovery of electron diffraction that De Broglie proposed the concept of wavelength λ of waves associated with particles like electrons and photons. If ‘p’ I the momentum of these particles then it is given by

λ = h/p = h/mv

The wavelength associated with an electron accelerated through a potential difference of V volt is given by

1/2 m_ev² = eV  or v = √2eV/m_e

The following video will provide more useful information on de-Broglie waves:-

Problem 1 (JEE Advanced):-

An electron and a photon have same wavelength. If p is the momentum of electron and E is the energy of photon. The magnitude of p/E in S.I unit is

(a) 3.010⁸              (b) 3.3310^-9

(c) 9.110^-31             (d) 6.6410^-34

Solution:-

As we know that, for electron, λ = h/p         

or, p = h/λ 

and for photon E = hc/λ

Thus, p/E = 1/c = 1/(310⁸ m/s)

= 3.33  10^-9 s/m

Therefore, from the above observation we conclude that, option (b) is correct. 

Problem 2:-

A particle of mass m is confined to a narrow tube of length L. Find

(a) The wavelengths of the de-Broglie wave which will resonate in the tube,

(b) The corresponding particle momenta, and

(c) The corresponding energies.

Solution:-

(a) The de Broglie waves will resonate with a node at each end of the tube.

A few of the possible resonance forms are listed below:

λ_n = 2L / n; = 1, 2, 3, ...

(b) Since de-Broglie wavelengths are

λ_n = h / p_n

∴  p_n = h / λ_n = nh / 2L            n = 1, 2, 3, ...

(c) (KE)_n = P_n² / 2m = n²h²/8L²m,   n = 1, 2, 3, ...  

Problem 3:-

What is the energy and wavelength of a thermal neutron?

Solution:-

By definition, a thermal neutron is a free neutron in a neutron gas at about 20°C (293 K).

KE= 3/2 kT = 3/2 (1.38 × 10^–23) (293) = 6.07 × 10^–21 J    

λ = h/p = h/√2m₀ (KE) = 6/63 × 10^–34/√2(1.67 × 10^–27) (6.07 × 10^–21) = 0.147 nm

Question 1

The de Broglie wavelength of a particle is the same as the wavelength of photon. Then, the photon’s energy is:

(a) equal to the kinetic energy of the particle.

(b) less than kinetic energy of the particle.

(c) greater than kinetic energy of the particle.

(d) nothing can be specified.

Question 2

The operation of the electron microscope depends on the

very short wavelength of X-rays

wave nature of electrons

electromagnetic theory of waves

photoelectric effect

Question 3

An electron and a proton have the same de Broglie wave length. Then the kinetic energy of the electron is

(a) zero  

(b) infinity

(c) equal to the kinetic energy of the proton

(d) greater than the kinetic energy of the proton 

Question 4

A nucleus of mass ‘M’ at rest emits an α-particle of mass ‘m’. The de Broglie wave lengths of the α-particle and residual nucleus will be in the ratio

(a) m : M           (b) (M+m) : m

(c) M : m             (d) 1 : 1

Question 5

The ratio of the de Broglie wave lengths of the electron in the first and the third orbits in the hydrogen atom is

(a) 1 : 1 (b) 1 : 3 (c) 1 : 9 (d) 1 : 6

Related Resources

• You might like to refer Bohr Model.

• For getting an idea of the type of questions asked, refer the  Previous Year Question Papers.

• Click here to refer the most Useful Books of Physics.

• To get answer to any question related to de-Broglie waves click here.