Dipole in Uniform External Field
Table of contents |
Introduction to Dipole in Uniform External Field
If a dipole is kept in an external electric field, it experiences a rotating effect. By external electric field, we mean electric field that is not induced by dipole itself. The rotating effect is also called torque on the dipole. How we can calculate the torque on a dipole and what are its applications? This can be done by calculating the net torque on opposite charges of the dipole.
Dipole in Uniform External Field
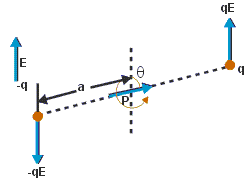
To find torque on a dipole from an external field, consider there is electric dipole
placed in an uniform external field
.The uniform external electric fieldis produced externally and is not induced by dipole.
Image 1: An electric dipole placed in non-uniform external electric field
The external electric field will produce electric force of magnitude qE on positive charge in upward direction and on negative charge in downward direction. We can see that the dipole is in transitional equilibrium as net force on the dipole is zero. What about the rotational equilibrium? Is it also zero? If that was the case, then the dipole would have been stationary in position, but experimentally it is found that the dipole rotates with some angular velocity.
This is because, both the electrostatic force that is, qE acts a torque in a clockwise direction, thereby making the dipole to rotate in a uniform external electric field.
Image 2: Uniform and Non-uniform electric field
Torque always acts in a couple, and its magnitude equals to the product of force and its arm. Arm is the distance between the point where the force acts and the point which rotates the dipole. In the dipole placed in the uniform external electric field, we take origin as the point. Torque is denoted by the symbol τ and as it has a direction, it is a vector quantity.
Mathematically,
Magnitude of torque = q E × 2a sin θ
τ = 2 q a E sin θ
τ = p E sin θ (Since p = 2 q a)
The vector form of torque is the cross product of dipole moment and electric field.
To understand what cross product is, let’s take an example.
Example:
Suppose there are two vectors
then cross product of two vectors will be
Cross product =
The direction of cross product is normal to both the vectorsand its magnitude can be evaluated as
Cross product = A B sin θ
where θ is the angle between two vectors.
So, the torque equation in vector form can be written as
Image 3: Torque rotates the dipole in uniform electric field
Observations in net force and torque
Taking the nature of electric field and position of the dipole, following remarks will come out:
-
If the dipole
and external electric field 
are parallel, that is, angle between them is zero, then the dipole will feel zero torque -
If the external electric field
is non-uniform, then net force on the dipole will not be zero, and torque will still act on it -
If the dipole external electric field
are antiparallel,that is, angle between them is non-zero, then the dipole will feel zero torque -
When the electric dipole
and electric field are parallel,the direction of net force will be in direction of increasing electric field
Image 4: Direction of net force depends on orientation of electric dipole
-
When the electric dipole
and electric field are anti-parallel, then the direction of net force will be in direction of decreasing electric field -
Force and Torque on a dipole placed in a uniform external field
varies with the orientation of dipole in free space
Physical Significance
When we comb our dry hair and bring it near to some paper pieces, we find that the comb attracts the paper pieces. The comb gains charge, from our hair by the process of rubbing and induce a charge in the uncharged paper. In another way, the comb polarizes the pieces of paper that is, generate a net dipole moment in the direction of electric field. Also since the electric field is non-uniform, the paper pieces move in the direction of the comb.
Watch this Video for more reference
More Readings