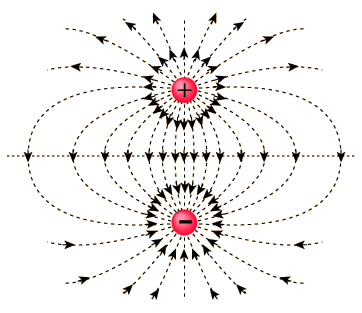
Electric Dipole
Table of contents |
Electric Dipole
Electric Dipole is defined as a couple of opposite charges q and –q, which are at 2a distance apart from each other. When we connect these two charges by a line, the line becomes responsible for the direction of the electric dipole in space. By default, the direction of the dipole is from negative charge –q to positive charge q. Also, the mid-point of q and –q is called Center of the Dipole.
Image 1: Electric Dipole
Mathematically, electric dipole is denoted by symbol
and equals to product of charge (only magnitude) and distance
between them. The magnitude ofis 2a.
The magnitude of dipole will be
p = 2aq
What will be the total charge of the dipole? Will it generate an electric field or not? As in a dipole both charges are of opposite sign, they will eventually cancel out, that is, net charge on the electric dipole is zero. But since there is the distance between them, the electric field will not be zero and yield some electric field.
Electric Field Due to Electric Dipole
Image 2: Electric Field due to electric dipole
The electric field due to a dipole that is, a pair of charges q and –q, can be evaluated easily from Coulomb’s Law and Superposition Principle. The field due to electric dipole is also called dipole field. The electric field due to a dipole at a point can be found in two cases:
-
When the point is axis of the dipole
-
When the point is in the equatorial plane of the electric dipole that is, perpendicular to the axis of the dipole, passing through the center
The net electric field due to dipole will be the vector sum of the electric field due to charge q and –q. Let the electric field due to positive charge q be EB and due to negative charge – q be
E-q.
On the axis
When the point is on the axis of dipole
Image 3: Electric Field along the axis of the dipole
Let there be a point P at a distance ‘r’ from the center of the dipole. Then electric field E-q ,due to negative charge –q will be
The electric field Eq due to positive charge q will be
The net electric field at point P will be the vector sum of both the electric fields.
Note: Since the electric fields are antiparallel, the vector sum will be:
Since r >>> a, we can neglect a with respect to r, then ( r2 – a2)2 becomes r4, then the net electric field becomes
On the equatorial plane
When the point is on the perpendicular bisector, of axis of dipole
Image 4: Electric Field due to electric dipole on the perpendicular bisector
The magnitude of electric field Eq at the point P, due to positive charge q will be
The magnitude of electric field E-q at the point P, due to negative charge q will be
Observing the diagram carefully, we find that vertical component of both electric fields that is, Eq sin θ and E-q sin θ will cancel out. Now, the horizontal components of both electric fields will add along the dipole, the net electric field, in this case, will be
Again neglecting a with respect to r, we get ( r2 + a2)3/2 to r3, therefore the net electric field can be written as
Since a dipole is a very small quantity, we find that electric field depends on both charge q and distance 2a, between them.
Using the dipole vector relation 
we can arrange the equation as
(a) On the axis of the dipole
(b) On the perpendicular bisector
Physical Significance of Electric Dipole
Apart from electrostatics, the electric dipole is quite significant in chemistry too. In most molecules, the center of positive and negative charge coincides at the same point, which means the distance between two charges is zero. So the dipole moment becomes zero. Carbon dioxide ( CO2) and Methane ( CH4) fall in this category of zero dipole moment. This type of molecules is called Non-polar Molecules. Some molecules develop electric dipole in presence of electric field.
Image 5: Electric Dipole of some chemical molecules
The molecules which have a permanent dipole moment, as the center of positive and negative charge don’t coincide.They are called Polar Molecules. For Example, Water H2O is a polar molecule.
Watch this Video for more reference
More Readings