Solved Examples on Hyperbola

Example:

Show that the line 4x – 3y = 9 touches the hyperbola 4x² – 9y² = 27.

Solution:

We know that if the line y = mx + c touches the hyperbola x²/a²–y²/b² = 1, then c²= a²m² – b²

Here the hyperbola is

x²/(27/4)–y²/(27/9) = 1

i.e. here a² = 27/4 b² = 27/9 = 3

And comparing 4x – 3y = 9 with y = mx + c, we get

‘m’ = 4/3, ‘c’ = –3

∴ a²m² – b² = (27/4)(4/3)³ – 3 = 12 – 3 = 9 = (–3)²

or a²m² – b² = c2

Hence the given line touches the given hyperbola.

Example:

Prove that the mid points of chords of the hyperbola x²/a²–y²/b² = 1 parallel to the diameter y = mx lie on the diameter a²my = b²x

Solution:

The hyperbola is x²/a²–y²/b² = 1 …… (1)

The equation of any chord parallel to the diameter

y = mx is y = mx + c …… (2)

Eliminating y between (1) and (2), we get

x²/a²–(mx+c)²/b² = 1

⇒ x²(b² – a²m²) – 2a²m cx – a²(b² + c²) = 0

⇒ b²x₃ = a²my₃

∴ The locus of (x₃, y₃) is

b²x = a²my Hence proved.

Example:

Prove that the angle subtended b any chord of a rectangular hyperbola at the centre is the supplement of the angle between the tangents at the end of the chord.

Solution:

Let the equation of the hyperbola be x² – y² = a² and P and Q be any two points on it such that their coordinates are respectively (a sec ?₁, a tan ?₁) and (a sec ?₂, a tan ?₂) and C be the centre of the hyperbola.

Equation of the line PC is y – 0 = atan?₁–0/asec?₁–0 (x – 0)

⇒ y = x sin ?₁ …… (1)

Similarly equation to QC will be y = x sin ?₂ …… (2)

If a be the angle between PC and QC, then

tan α = sin?₁–sin?₂/1+sin?₁sin?₂ …… (3)

Again the equation to the tangent at P is

x a sec ?₁– y a tan ?₁ = a²

y = x/sin?₁ – acos?₁/sin?₁ …… (4)

Similarly the equation to the tangent at Q₂ is

y = x/sin?₂ – a cos?₂/sin?₂

If b be the angle between the tangents at f₁ and f₂, then

tan ß = 1/sin?₂ 1/sin?₂/1+1/sin?₁ 1/sin?₂ = sin?₂–sin?₁/1+sin?₁sin?₂

= –(sin?₁–sin?₂)/1+(sin?₁sin?₂)

⇒ tanß = –tanα

⇒ tanß = tan (π – α) (By (3))

⇒ ß = π – α Hence proved.

Solved Examples of Hyperbola Part-II

Example:

The normal to the hyperbola 16x² – 9y² = 144 meets the axes in M and N. MP and NP and are drawn at right angles to the axes. Find the locus of P.

Solution:

The equation to the hyperbola is

x²/a² – y²/b² = 1 …… (1)

Let L be any point on it having the coordinates (3 sec ?, 4 tan ?) then the equation to the normal at this point will be given by

3x sin ? + 4y = (9 + 16) tan ? …… (2)

Let this normal cut the axis of x at M whose coordinates are (x, 0) and the axis of y at N whose coordinates are (0, y) solving (2) with y = 0, we get

x = 9+16/3cos? = 25/3cos? …… (3)

941_Parallel lines to the axes.JPG

Similarly solving (2) with x = 0, we get

y = (9+16)tan?/4 = 25tan?/4 ……(4)

If PM and PN be the lines parallel to the axes, the coordinates of

P = (x, y) will be clearly given by (3) and (4). The required locus of P will be obtained by eliminating ? from (3) and (4).

Using the fact sec² ? – tan² ? = 1, we get

9x² – 16y² = 625

Example:

Prove that a circle can be drawn through the foci of a hyperbola and the points at which any tangent meets the tangents at the vertices of the hyperbola.

Solution:

Recall:

If four points (x₁, y₁), (x₂, y₂), (x₃, y₃) and (x₄, y₄) are concyclic then

824_Matrix 2.JPG

These points are (ae, 0), (–ae, 0), (a, b tan ?/2) and (–a, –b cot f/2)

2315_Matrix 3.JPG

apply : R₁ → R₁ – R₂ and expand along R₁, we get

= (–2ae)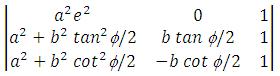

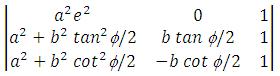
= (–2aeb) [(a² e² – a² – b²) cot ?/2 + 9a²e² – b² – a²) tan ?/2] = 0

∴ points S, S’, R and Q are conclycic.

Example:

On a level plain the crack of the rifle and the thud of the ball striking the target are heared at the same instant, prove that the locus of the hearer is a hyperbola.

Solution:

Suppose A to be the target and B to be the firing point and let the hearer be at a point P. If V₁ and V₂ be the velocity of the sound and bullet respectively, then the time taken by the bullet in reaching from B to the target A = BA/v₂ and the time taken by the sound in reaching from A to P = AP/v₁.

Again the time taken by the sound in reaching from B to P = BP/v₁.

As by hypothesis the sound reaches the hearer at P, simultaneously, the time taken by the sound to reach upto the position P from then target together with the time taken by the bullet to reach the target must be same as the time taken by the sound in reaching from the rifle upto P.

Hence BA/v₂ + AP/v₁ = BP/v₁

⇒ BA/v₂ = BP/v₁ – AP/v₁ = 1/v₁ (BP – AP)

⇒ BP – AP = v₁/v₂ AB

As v₁, v₂ and AB are constants, hence

BP –AP = Constant

Therefore the locus of the point P is the hyperbola having foci at A and B and transverse axis equal to v₁/v₂ AB

Example:

Prove that the locus of the pole of a chord of the hyperbola which subtends a right angles at the vertex, is, x = a²–b²/a²+b².

Solution:

The coordinates of the vertex are (a, 0). Transferring the origin to this point, the equation of the hyperbola x²/a²–y²/b² becomes;

(x+a)²/a²– y²/b² = 1

⇒ x²/a²–y²/b² = –2x/a

⇒ b²x² – a²y² = –2ab²x …… (1)

The equation to the polar of (h, k) w.r.t hyperbola is given by

b²hx – a²hky = a²b² …… (2)

After transformation the equation (2) becomes

b²(x + a)h – a²yk = a²b²

or b²hx – a²yk = a²b² – ab²h …… (3)

The equation of the lines joining the points of intersection of the hyperbola and the chord to the origin is obtained by making (1) homogeneous with the help of (3). Hence on simplification, this equation becomes

(a²b² – ab²h) (b²x² – a²y²) = –2ab²x(b²xh – a²yk)

If they are at right angles, the sum of the coefficients of x² and y² must be zero; hence

b² – a² + 2b²h/a–h = 0

generalizing for (h, k), we get the required locus as

x = a a²–b²/a²+b²

Example:

Find the locus of intersection of tangent to a hyperbola, which meet at a constant angle ß.

Solution:

Let the equation to the hyperbola be

x²/a²–y²/b² = 1 …… (1)

Equation to any tangent to (1) is

y = mx + √a²m²–b²

If the tangent passes through a point (h, k) when we must have

k = mh + √(a²m²–b²)

or m²(h² – a²) – 2mhk + (k² + b²) = 0 …… (2)

Let m₁ and m₂ be the two roots of this equation.

⇒ m₁ = tanθ₁ and m₂ = tanθ₂, we have

tanθ₁ + tanθ₂ = 2hk/h²–a²

tanθ₁ × tanθ₂ = k²+b²/h²–a²

and as (tanθ₁ – tanθ₂)² = 4h²k²–4(k²+b²)(h²–a²)/(h²–a²)².

= 4(a²k²–b²h²+a²b²)/(h²–a²)²

If the two tangents met at an angle ß, clearly ß = (θ₁ – θ₂).

Hence cotß = cot(θ₁ – θ₂)

= 1/tan(θ₁–θ₂) = 1+tanθ₁tanθ₂/tanθ₁–tanθ₂

⇒ cot²ß = (1+tanθ₁tanθ₂)²/(tanθ₁–tanθ₂)² = (h²+k²+b²–a²)²/4(a²k²–b²h²+a²b²)²

Simplifying, the required locus is

(x² + y² + b² – a²)² = 4cot²b(a²y² – b²x² + a²b²)²

Example:

Find the equation to the hyperbola whose asymptotes are the straight lines x + 3y – 1= 0 and 2x – y + 7 = 0, and which passes through the point (1, 2).

Solution:

Equation to the asymptotes are given as

x + 3y – 1 = 0 and …… (1)

2x – y + 7 = 0 …… (2)

(1) and (2) may be given by

(x + 3y – 1)(2x – y + 7) = 0 …… (3)

As the equation to the hyperbola will differ from (3) only by a constant, it may be given by

(x + 3y – 1)(2x – y + 7) = λ …… (4)

(where λ is a constant)

(1, 2) lies on the curve given by (4), we have

(1 + 6 – 1)(2 – 2 + 7) = λ

⇒ λ = 42

Hence the equation to the hyperbola will be

(x + 3y – 1)(2x – y + 7) = 42

⇒ 2x² – xy + 6xy + 7x – 3y² + 21y – 2x + y – 7 = 42

⇒ 2x² – 3y² + 5xy + 5x + 22y – 49 = 0

Solved Examples of Hyperbola Part-III

Example:

Prove that the locus of the pole of a chord of the hyperbola which subtends a right angles at the vertex, is, x = a²–b²/a²+b².

Solution:

The coordinates of the vertex are (a, 0). Transferring the origin to this point, the equation of the hyperbola x²/a²–y²/b² becomes;

(x+a)²/a²– y²/b² = 1

⇒ x²/a²–y²/b² = –2x/a

⇒ b²x² – a²y² = –2ab²x …… (1)

The equation to the polar of (h, k) w.r.t hyperbola is given by

b²hx – a²hky = a²b² …… (2)

After transformation the equation (2) becomes

b²(x + a)h – a²yk = a²b²

or b²hx – a²yk = a²b² – ab²h …… (3)

(a²b² – ab²h) (b²x² – a²y²) = –2ab²x(b²xh – a²yk)

If they are at right angles, the sum of the coefficients of x² and y² must be zero; hence

b² – a² + 2b²h/a–h = 0

generalizing for (h, k), we get the required locus as

x = a a²–b²/a²+b²

Example:

Find the locus of intersection of tangent to a hyperbola, which meet at a constant angle ß.

Solution:

Let the equation to the hyperbola be

x²/a²–y²/b² = 1 …… (1)

Equation to any tangent to (1) is

y = mx + √a²m²–b²

If the tangent passes through a point (h, k) when we must have

k = mh + √(a²m²–b²)

or m²(h² – a²) – 2mhk + (k² + b²) = 0 …… (2)

Let m₁ and m₂ be the two roots of this equation.

⇒ m₁ = tanθ₁ and m₂ = tanθ₂, we have

tanθ₁ + tanθ₂ = 2hk/h²–a²

tanθ₁ × tanθ₂ = k²+b²/h²–a²

and as (tanθ₁ – tanθ₂)² = 4h²k²–4(k²+b²)(h²–a²)/(h²–a²)².

= 4(a²k²–b²h²+a²b²)/(h²–a²)²

If the two tangents met at an angle ß, clearly ß = (θ₁ – θ₂).

Hence cotß = cot(θ₁ – θ₂)

= 1/tan(θ₁–θ₂) = 1+tanθ₁tanθ₂/tanθ₁–tanθ₂

⇒ cot²ß = (1+tanθ₁tanθ₂)²/(tanθ₁–tanθ₂)² = (h²+k²+b²–a²)²/4(a²k²–b²h²+a²b²)²

Simplifying, the required locus is

(x² + y² + b² – a²)² = 4cot²b(a²y² – b²x² + a²b²)²

Example:

Find the equation to the hyperbola whose asymptotes are the straight lines x + 3y – 1= 0 and 2x – y + 7 = 0, and which passes through the point (1, 2).

Solution:

Equation to the asymptotes are given as

x + 3y – 1 = 0 and …… (1)

2x – y + 7 = 0 …… (2)

(1) and (2) may be given by

(x + 3y – 1)(2x – y + 7) = 0 …… (3)

As the equation to the hyperbola will differ from (3) only by a constant, it may be given by

(x + 3y – 1)(2x – y + 7) = λ …… (4)

(where λ is a constant)

(1, 2) lies on the curve given by (4), we have

(1 + 6 – 1)(2 – 2 + 7) = λ

⇒ λ = 42

Hence the equation to the hyperbola will be

(x + 3y – 1)(2x – y + 7) = 42

⇒ 2x² – xy + 6xy + 7x – 3y² + 21y – 2x + y – 7 = 42

⇒ 2x² – 3y² + 5xy + 5x + 22y – 49 = 0

To read more, Buy study materials of Hyperbola comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.