Magnetic Dipole

Table of Content

Magnetic Dipole Moment
- Magnetic dipole in a Uniform Field Magnetic Field
Units of M
Work done in Rotating a Magnetic Dipole in a Magnetic Field
Potential Energy of a Magnetic Dipole in a Magnetic Field
Current Loop as a Magnetic Dipole
The Magnetic Dipole Moment of a Revolving Electron
Related Resources

The limit of a closed loop of electric current is defined as a magnetic dipole. The structures, which tend to align along the direction of magnetic field, are known as magnetic dipoles. A current loop creates as well as responds to magnetic fields. We first examine the torque felt by a dipole in a magnetic field. Consider the current loop in a magnetic field in the figure given below. The two forces which are equal and opposite do not act to bring about a movement in the dipole, but only rotate it.

A combination of two isolated, equal and opposite magnetic poles separated by a small distance constitutes a magnetic dipole. The distance between two magnetic poles is known as magnetic length and is denoted by 2l. A line passing through the north and south poles of a magnetic di-pole gives the axial line of the magnetic dipole.

A line passing through a point mid-way between the two poles of a magnetic dipole and perpendicular to its axial line gives the equatorial line of the magnetic dipole. The axial line and the equatorial line of the magnetic di-pole are shown in below figure.

Magnetic Dipole Moment

Magnetic dipole moment is the measure of the ability of a dipole to convert itself and come into alignment with a given external magnetic field. It may also be defined as the maximum expanse of torque caused by magnetic force on a dipole that ascends per unit value of surrounding magnetic field in vacuum. In case of a uniform magnetic field, the magnitude of the dipole moment is proportional to the maximum quantity of torque on the dipole. This generally occurs when the dipole is at right angles to the magnetic field.

Magnetic dipole in a Uniform Field Magnetic Field

Consider a uniform magnetic field of strength B. Let a magnetic dipole be suspended in it such that its axis makes an angle θ with the field as shown in figure. If ‘m’ is the strength of each pole, the two poles N and S experience two equal and opposite forces ‘mB’. These forces constitute a couple which tends to rotate the dipole. Suppose the couple exerts a torque of magnitude $\tau$ .

$\tau$ = (either force) $\times$ (perpendicular distance between the two forces)

= mB $\times$ AC = mB $\times$ 2l sin θ

Or $\tau$ = MB sin θ

Here, M = 2ml = magnetic moment of the dipole

If B = 1 and θ = 90º

$\tau$ = M

Magnetic moment M of the magnetic dipole is defined as the moment of the couple acting on it when it is placed at right angles to a uniform field of unit strength.

In such case,

Force on each pole = m $\times$ 1

Perpendicular distance between two forces = NS = 2l

So, $\tau$ = m $\times$ 2l

Thus, magnetic moment of a magnetic dipole is also defined as the product of its pole strength and the magnetic length.

Magnetic moment of a magnet is a vector quantity and is directed along SN inside the magnet.

$\vec{M} = M\hat{l}$

Here, $\hat{l}$ = unit vector along SN.

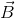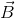Since $\vec{M}$ and $\vec{B}$ , both, are vectors the torque acting on a magnet suspended in the magnetic field can be expressed as the cross-product of $\vec{M}$ and $\vec{B}$ as follows.

$\vec{\tau }=\vec{M}\times \vec{B}$

The direction of $\vec{\tau }$ can be obtained by applying right hand thumb rule.

Units of M

Units of M can be obtained from the relation

$\tau$ = MB sin θ

So, M = $\tau$ /B sin θ

Therefore, M can be measured in terms of joule per tesla (JT^-1) or (NmT^-1)

Since ,1 tesla = Wb/m²

Thus, Unit of M = J/(Wb/m²) = Jm²/Wb

Since 1 J = 1 Nm

Therefore, Unit of M = 1 Nm T^-1 = 1 Nm/(Wb/m²) = 1 Nm³ Wb^-1

Since unit of pole strength = Am

Thus, Unit of M = (Am) m = Am²

Work done in Rotating a Magnetic Dipole in a Magnetic Field

When a magnetic dipole of magnetic moment M is oriented in a magnetic field of strength, B, making an angle ‘θ’. With its lines of force, it experiences a torque $\tau$ given by

$\vec{\tau } = \vec{M}\times \vec{B}$

$\left | \vec{\tau } \right | = MB sin\theta$

Let $d\vec{\theta }$ be the small abgular displacement given to the dipole, work done dW is given by

$dW = \vec{\tau }.d\vec{\theta } = \tau d\theta$

Since the angle between $\vec{\tau }$ and $d\vec{\theta }$ is zero.

So, dW = MB sin θ dθ

Work done in displacing the dipole from an angle θ₁ to θ₂ is

$W = \int_{0}^{W} dW = \int_{\theta _{1}}^{\theta _{2}}MB sin\theta d\theta$

W = MB [(-cos θ₂) – (- cos θ₁)]

Or, W = MB (cos θ₁ – cos θ₂)

Potential Energy of a Magnetic Dipole in a Magnetic Field

Potential energy of a magnetic dipole, in a magnetic field, is defined as the amount of work done in rotating the dipole from zero potential energy position to any desired position.

It is convenient to choose the zero potential energy position to be the one when the dipole is at right angles to the lines of force of magnetic field.

So, θ₁ = 90º and θ₂ = θ

Making these substitution in equation (3), we get,

Potential energy = W = MB (cos 90º – cos θ)

Or, W = – MB cosθ

In vector form, $W = - \vec{M}.\vec{B}$

Special cases:

(a) When θ = 0º, cos θ = 1

So, W = – MB

(b) When θ = 90º, cos θ = 0

So, W = – MB(0) = 0

So, W = – MB (-1) = MB

θ = 0º position corresponds to the position of dipole aligning itself such that its magnetic moment vector $\vec{M}$ is parallel to field. In this case, potential energy is – MB, a minimum value. We know that every body in state of equilibrium must possess minimum potential energy. That is why the magnetic dipole exists in equilibrium when $\vec{M}$ is parallel to $\vec{B}$ .

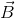Refer this simulation to know more about alignment of magnetic domain

[Note: Please click on “red circle” to run the simulation]

This illustrates the fact that domains line up with a magnetic field and some metals, such as iron, partially retain the new domain alignment.

Current Loop as a Magnetic Dipole

Ampere found that the distribution of magnetic lines of force around a finite current carrying solenoid is similar to that produced by a bar magnet. This is evident from the fact that a compass needle when moved around these two bodies show similar deflections. After noting the close resemblance between these two, Ampere demonstrated that a simple current loop behaves like a bar magnet and put forward that all the magnetic phenomena is due to circulating electric current. This is Ampere’s hypothesis.

The magnetic induction at a point along the axis of a circular coil carrying current is,

B = µ_onIa²/2(a²+x²)^3/2

The direction of this magnetic field is along the axis and is given by right hand rule. For points which are far away from the centre of the coil, x>>a, a² is small and it is neglected. Hence for such points,

B = µ_onIa²/2x³

If we consider a circular loop, n = 1, its area A = πa²

So, B = µ_oIA/2πx³

The magnetic induction at a point along the axial line of a short bar magnet is

B = (µ_o/4π) (2M/x³)

Or, B = (µ_o/2π) (M/x³)

Comparing equations (1) and (2), we find that

M = IA

Hence a current loop is equivalent to a magnetic dipole of moment M = IA

The magnetic moment of a current loop is defined as the product of the current and the loop area. Its direction is perpendicular to the plane of the loop.

Watch this Video for more reference

The Magnetic Dipole Moment of a Revolving Electron

According to Neil Bohr’s atom model, the negatively charged electron is revolving around a positively charged nucleus in a circular orbit of radius r. The revolving electron in a closed path constitutes an electric current. The motion of the electron in anticlockwise direction produces conventional current in clockwise direction.

Since the electron is negatively charged, conventional current flows in a direction opposite to its motion. The magnetic moments associated with the two types of motion of electron in an orbit are shown in figure. An electron revolving in an orbit of radius ‘r’ is equivalent to a magnetic shell of magnetic moment ‘M’ given by

M = i $\times$ A

Here ‘i’ is the current to which the rotating electron is equivalent to and A is the area of the orbit. If ‘ $\tau$ ’ is the time period of rotation of electron.

i = charge/period = e/ $\tau$ = e/(2π/ω)

or i = eω/2π

Here, ‘ω’ is the angular velocity of the electron.

So, M = (eω/2π) $\times$ (πr²) = eωr²/2

According to Bohr’s theory, an electron can revolve in an orbit in which its angular momentum is an integral multiple of h/2π where ‘h’ is Planck’s constant.

mr²ω = n (h/2π)

Or, r²ω = n (h/2πm)

Substituting for r²ω in equation (4), we get,

M = n (eh/4πm)

Since an atom may have a large number of electrons, the resultant magnetic moment of the atom is the vector sum of the magnetic moments of various electrons.

The term eh/4πm is called Bohr’s magneton. It is the smallest value of magnetic moment which an electron possess. Any atom can possess magnetic moment which is an integral multiple of Bohr’s magneton. Thus, the magnetic moment is also quantised in the atomic and sub-atomic level.

In addition to the magnetic moment due to its orbital motion, the electron possesses magnetic moment due to its spin. Hence the resultant magnetic moment of an electron is the vector sum of its orbital magnetic moment and its spin magnetic moment.

An isolated magnetic pole is non-existent. Whenever we break a magnet we obtain two complete magnets.
A magnet when freely suspended, always points geographic north-south direction.
Magnetic length is nearly 7/8 times the geometric length.
A uniform magnetic field is represented by equidistant parallel lines of force.
Magnetic moment of a magnet is a vector quantity. Its direction is from S to N.
Magnitude of magnetic moment is equal to the product of pole strength and magnetic length.
It is not possible to separate out the two poles of a magnet.
Magnetic dipole is not a system composed of two poles because the existence of monopoles is not possible.
A loop of single turn is also a magnetic dipole. One face of the loop behaves as North Pole and the other face behaves as South Pole. The face of the coil, in which current is anticlockwise, behaves as north pole and the face in which current is clockwise, behaves as south pole.

Problem (JEE Main):

A uniformly charged disc of radius r and having charge q rotates with constant angular velocity ω. The magnetic dipole moment of this disc is 1/n (qωr²). Find the value of n.

We know that, M/L = q/2m

So, M = qL/2m = q(Iω) / 2m

= [q (1/2 mr²) ω] / 2m

= ¼ qωr²

Therefore, from the above observation we conclude that, the value of n will be 4.

Question 1

A magnetic needle lying parallel to a magnetic field requires W units of work to turn it through 60°. The torque needed to maintain the needle in this position will be,

(a) √3 W (b) W

Question 2

The magnetic induction, in air, at a distance d from an isolated point pole of strength m unit will be,

(a) m/d (b) m/d²

Question 3

A magnet of moment M is suspended in a uniform magnetic field B. The maximum value of torque acting on the magnet is

(a) MB (b) ½ MB

Question 4

Magnetic field due to a short magnet of magnetic moment M at a distance d from its centre in the end on position is

(a) M/d² (b) M/d³

Question 5

A magnetic dipole is placed in the position of stable equilibrium in a uniform magnetic field of induction B. If it is rotated through an angle 180º, then the work done is

(a) MB (b) 2 MB

Q.1	Q.2	Q.3	Q.4	Q.5
a	b	a	d	b

Related Resources

You might like to magnetic moment.
For getting an idea of the type of questions asked, refer the Previous Year Question Papers.
Click here to refer the most Useful Books of Physics.
To get answer to any question related to magnetic dipole click here.

Live courses Ask question