Conic Sections
Table of Content |
|
|
The first definition of conic section was given by Menaechmus but his work didn’t work. The Apollonius of perga had written about the conic sections and the other hidden discoveries of conics in his book “The conic” in 200 B.C. Archimedes and Apollonius had studied the conics for their own beauty but now it is very important tool in space and research work.
Meaning of Conic Sections
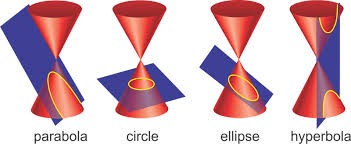
Conic Section is a curve formed by the intersection of a plane with the two napped right circular cone. Because of this intersection, different types of curves are formed due to different angles. Or you can say that if we slice the 3d cone in pieces it could be cut in different shapes and these shapes form some curves these are called Conic Sections, sections here means the slice of cone.
What is a right circular cone?
There are two lines intersect each other at a fixed point and angle. One line rotates around it so that the angle remains the same and the surface obtained then is called the Right Circular Cone.
Terms used in Conic Sections
To understand the conic sections first we need to understand some terms which are used in it:
-
Center - The point at the center of a circle, an ellipse or a hyperbola. There is no center in parabola.
-
Vertex - The right circular cone consists of two cones joint at a fixed point is called Vertex (represented as V in the above picture).
-
Generator – The line which rotates around is called Generator as shown by orange line in the picture.
-
Axis - A line which is fixed and perpendicular to the base and passes through the vertex is called Axis.
-
Directrix- The perimeter of the base is called the Directrix.
-
Nappe - The lateral surface or the round surface of the cone is called the Nappe. The nappe above the vertex is called the upper nappe and the nappe below the vertex is called the Lower Nappe.
Vertex Angle – The angle between the axis and the generator is called the Vertex Angle.
-
Focus - It is a point from which the distance is measured to form conic.
-
Major Axis- It is a line segment which is perpendicular to the directrix of any conic section.
-
Minor Axis - It is a line segment which is perpendicular to the directrix and bisecting the major axis of the conic section.
-
Plane - The conic sections are the curves obtained when the plane intersects with the cone as shown in the above picture
Sections of a Cone
The conic sections are the curve obtained when the plane intersects with the cone .It is the angle of intersection which defines the type of conic sections. There are four types of conic sections.
-
Ellipse- When the plane intersects with the double circular cone in such a way that the angle between the axis and the plane is greater than the vertex angle then it made an ellipse.
-
Circle - When the plane is perpendicular at the axis, the ellipse becomes the circle. Or you can say that circle is the special type of ellipse.
-
Parabola- When the angle between the vertical axis and the plane is equal to the vertex angle, we get an open curve called parabola at the intersecting surface of the cone.
-
Hyperbola - In all the above conic sections we are getting one curve in only one nappe of the double cone, but when the angle between the plane and the vertical axis is less than the vertical angle, the plane intersects both the nappes of the cone which form two disjoint open curves are called Hyperbola.
Degenerate Conics
If a plane intersects the double right circular cone at the vertex then the ellipse become point, parabola becomes line and hyperbola becomes two intersecting lines.
Eccentricity
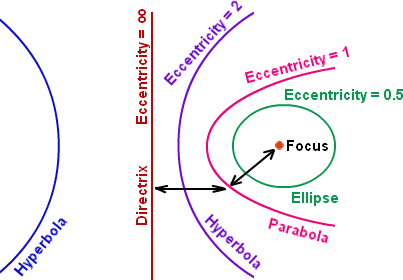
Eccentricity is the factor related to conic sections which shows how circular the conic sections. More the eccentricity less circular the shape is and more the eccentricity less circular the shape is. The eccentricity of the line is ∞. The two conic sections will be of same shape if they have same eccentricity. A conic section is defined as the locus of all points whose distances to a point (the focus) and a line (the directrix) are in a constant ratio. This ratio is called Eccentricity. It is denoted by“e”.
Eccentricity of circle is 0.
Eccentricity of ellipse is 0 < e <1.
Eccentricity of parabola e = 1.
Eccentricity of hyperbola e > 1.
Latus Rectum
It is the line parallel to directrix and passes through focus.
-
In a parabola latus rectum is four times the focal length.
-
In a circle, it is the diameter
-
In an ellipse, is 2b2/a (where a and b are one half of the major and minor diameter).
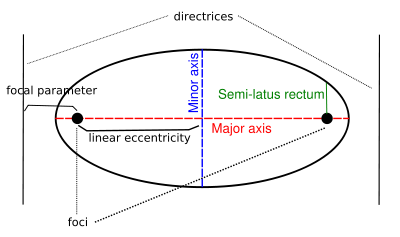
Conic Parameters
Some factors of conic sections are:
-
The line joining the foci of the ellipse or hyperbola is the principal axis and the center is the midpoint of the line segment.
-
The distance between the center and any of the focus is the linear eccentricity. It is denoted by “c”.
-
The latus rectum is the line segment parallel to directrix and passes through any of the focus. It is denoted by “2l”.
-
The half length of the latus rectum is called Semi Latus Rectum and it is denoted by “l”.
-
The distance between the focus and the directrix is the focal parameter. It is denoted by “p”.
-
The value of the semi major axis is a.
What is Cartesian coordinates?
To draw any graph we must know the points on a graph to show where we are on that map, these points are called the Cartesian coordinates.
The horizontal line is generally represented with “x” and the vertical line is represented with “y” and where x and y intersects is the “0” point i.e. we measure everything from there.
We represent the coordinates as (x, y). As shown in the picture on the right (0, 0) is the point where x and y intersects.
In the point (2, 3), x is 2 so we will start from 0 and move horizontally towards the point 2 and y is 3 so we will move vertically toward 3, then we will mark a point where these points intersects.
Likewise if there is any negative coordinate the we will move toward left if x is negative and downwards if y is negative.
Standard form of equations in Cartesian coordinates
The above conic parameters are used to create the standard form of conic sections.
The general Cartesian form of equation covering all the conic sections is-
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
Where all the coefficients are the real numbers.
But all the conic sections have some standard equations-
Circle
The standard form of a circle is:
(x - h)2 + (y - k)2 = r2
where (h, k) is the centre of the circle and r is the radius of the circle.
Its general form is
x2 + y2- hx – ky – (h + k) = 0
Ellipse
The standard form of an ellipse is:
where (h, k) is the centre of the ellipse, a is the horizontal stretch factor and b is the vertical stretch factor.
Parabola
x = a(y - k)2 + h (east to west), where a is the horizontal stretch factor or
y = a(x - h)2 + k (north to south), where a is the vertical stretch factor.
Hyperbola
where a is the horizontal stretch factor and b is the vertical stretch factor.
Classifying a conic from its equation
For the general second degree equation, that is,
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
The expression B2 - 4AC is the discriminant which is used to determine the type of conic section represented by equation.
| Discriminant | Type of conic |
| B2 - 4AC < 0,B = 0 and A = C | Circle |
| B2 - 4AC < 0,either B ≠ 0 or A ≠ C | Ellipse |
| B2 - 4AC = 0 | Parabola |
| B2 - 4AC > 0 | Hyperbola |
Example
Classify the following equations according to their type of conics.
A) 4x2 + 4y2 -16x + 4y - 60 = 0
B) x2 - 4x + 16y + 17 = 0
C) x2 + 2y2 + 4x + 2y – 27 = 0
D) x2 – y2 + 3x – 2y – 43 = 0
Solution
A) Here A = 4, B = 0, C = 4
Determinant will be B2 - 4AC
= 02- 4(4) (4) = -64
This shows that B2 - 4AC < 0, B = 0 and A = C, so this is a circle.
In other way we can say that both variables are squared, and both squared terms are multiplied by the same number, so this is a circle
B) Here A =1,B = 0, C = 0
Determinant will be B2- 4AC
= 02-4(1) (0) = 0
This shows that B2 - 4AC = 0, so this is a parabola or you can say that if Only one of the variables is squared, this is called a Parabola.
C) Here A =1, B = 0, C = 2
Determinant will be B2 - 4AC
= 02 - 4(1) (2) = -8
This shows that B2 - 4AC < 0, and A ≠ C so this is an ellipse or in other way we can say that Both variables are squared with the same sign, but they aren't multiplied by the same number, so this is an ellipse.
D) Here A =1,B = 0, C = -1
Determinant will be B2- 4AC
= 02 - 4(1) (-1) = 8
This shows that B2 - 4AC > 0 so this is a hyperbola or we can say that both variables are squared, and the squared terms have opposite signs, so this is a hyperbola.
Watch this Video for more reference
More Readings